Introduction
최근 10여년간 도시 및 농촌 중소하천의 건천화 현상이 중요한 사회문제로 주목을 받고 있다. 하천건천화 방지를 위해서는 건천화를 예방하고 관리할 수 있는 인프라 구축이 필요하며 특히 건천화 진행여부를 파악하는 과정이 필수적일 것이다. 그러나 하천건천화는 그 과정을 명확하게 관측하기가 쉽지 않고, 이를 유발하는 요인들이 복합적이기 때문에 이에 관한 정량적인 접근이 매우 어렵다(Jung et al., 2003). 이러한 하천건천화 진행여부의 보다 정확한 판단을 위해서는 중소규모 하천에 대한 지속적인 유량측정이 이루어 져야 하나 현재까지 국내에서 중소하천에 대한 유량관측 자료는 매우 부족하며(Ministry of Science and Technology, 2003), 따라서 건천화 진행 여부를 과거 자료만을 근거로 하여 파악하는 것은 현실적으로 매우 어려운 실정이다.
하천건천화의 주요 원인은 주로 도시개발로 인한 불투수면적의 증대, 지하수 개발, 대규모 하수종말처리장 건설, 치수위주의 하천정비 등을 들 수 있다. 이 중 지하수 이용과 하천수량과의 상관관계를 규명하기 위해서는 하천과 대수층의 상호작용을 명확하게 밝힐 필요가 있다. Kim et al. (2004)은 자연적인 상태에서 지표유량 변화를 계측하여 지하수와 지표수간의 상호작용을 해명하고자 하였으며, Kim et al. (2012a)은 관측자료를 근거로 낙동강 하류지역의 지하수위 변동의 특성을 분석하고자 하였다. Kim et al. (2012b)는 유역모형과 지하수 모형을 결합한 SWAT-MODFLOW를 이용하여 복하천 지류인 신둔천 유역에 대해 지하수 이용에 따른 하천수 감소량을 모의하였으며, Lee et al. (2016)은 지하수 모델링을 통한 수치실험으로 계절양수가 하천건천화에 미치는 영향을 파악하고자 하였다.
지하수 양수가 하천건천화에 미치는 영향 이외에도 Lee et al. (2006)은 기상자료, 지하수 취수량, 토지이용자료를 이용하여 구축한 회귀모형을 바탕으로 이들의 변화가 건기 총유출량에 미치는 영향을 분석하고자 하였다. 또한 Lee et al. (2013)은 고성군에 위치한 건천화 구간에 대한 현장조사를 통해 건천화 된 하천의 시공간적 특성을 분석하였으며, Jun et al. (2012)은 과거와 현재의 유출특성을 고려하여, 중소규모 하천 또는 도시하천의 건천화를 정량적으로 평가할 수 있는 지표를 제안하였다. Jung and Kim (2018)은 최근 Unmanned Aerial Vehicle (UAV)를 활용하여 하천건천화를 모니터링 하고자 시도하고 있으며, Kim et al. (2017)은 기상, 토양심, 산림높이, 도로망, 지하수이용량, 토지이용과 같이 하천건천화에 영향을 미칠 것으로 예상되는 다양한 요소들을 종합적으로 고려하여 건천화의 원인을 추적하고자 하고 있다. Park and Cho (2018)은 평상시 강수량, 연속무강수 일수, 유역면적, 하천수 취수량, 회귀수, 지하수 이용량, 토지피복도, 유지용수 공급댐의 8가지 항목을 선정하여 건천화 지표 및 건천화 잠재지수를 산정하였다.
상기에 서술한 연구들은 과거에 관측된 자료들을 활용하여 건천화의 진행을 파악하고자 하거나, 지하수 양수의 영향만을 고려한 모형을 기반으로 하여 건천화를 분석하고자 하였다. 하지만 전술하였듯이 중소하천의 자료는 충분하지 않은 경우가 많으며, 따라서 하천건천화의 원인은 복합적으로 도시개발로 인한 토지이용의 변화, 지하수 개발, 하천정비 등의 영향을 모두 반영할 수 있는 모형의 개발이 필요하다. 본 연구에서는 이러한 상황을 고려하여 건천화 해결을 위한 정책과 사업의 추진 시에 합리적 의사결정을 뒷받침할 수 있는 과학적 도구로서 유역수문변화를 고려한 장단기 분포형 수문모델을 개발하였다. 도시개발로 인한 토지이용변화, 지하수 양수, 하천정비 등을 모두 반영하여 유역을 물수지 및 건천화 상황을 모의할 수 있도록 모형을 개발하고자 하였다.
Materials and methods
모형의 기본 구조
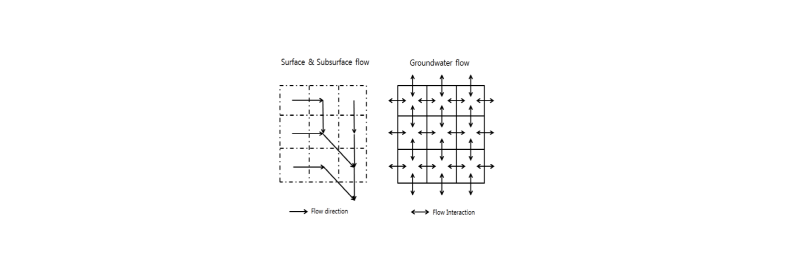
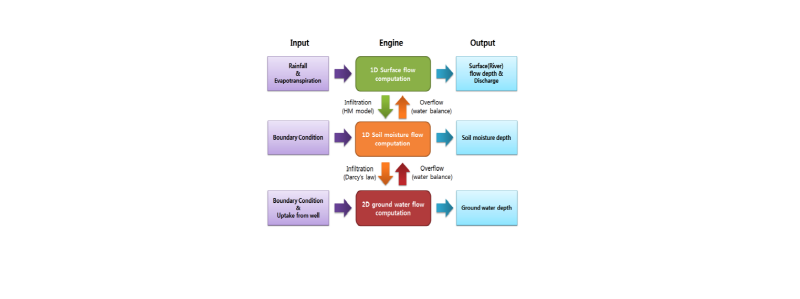
유역의 수문변화를 고려한 전지점 강우유출 모의를 위해서 본 연구에서는 Kim (1995)와 Kim and Chung (1995)에 의해 개발된 격자단위 물수지 개념을 채택하여 기본으로 임의지점의 시간별 저류량의 변화를 재현할 수 있는 강우-유출관계를 정립하였다. 하나의 격자는 Fig. 1과 같이 지표류층, 지표하흐름층, 지하수층 세개의 층으로 나뉘어 지며 각각의 층들은 이웃한 층과 상호작용을 하도록 모형을 설계하였다. 각각의 층은 개별적인 지배방정식에 따라 해석되고 타 층간의 물의 이동은 개별 격자에서 이루어 진다. 지표 및 지표하 흐름은 전통적인 격자단위 분포형 수문모형에서 사용하는 흐름누적도에 따라 8방향으로 격자간 흐름 이동을 해석하고 지하수는 Fig. 2에서처럼 인접 격자간 흐름 교환으로 해석한다. 지표 및 지표하 흐름은 1차원 수문해석이라고 할 수 있으며, 지하수 흐름은 2차원 수리해석을 사용하고 있다. 이를 구현하는 모델의 기본구조는 Fig. 3과 같다.
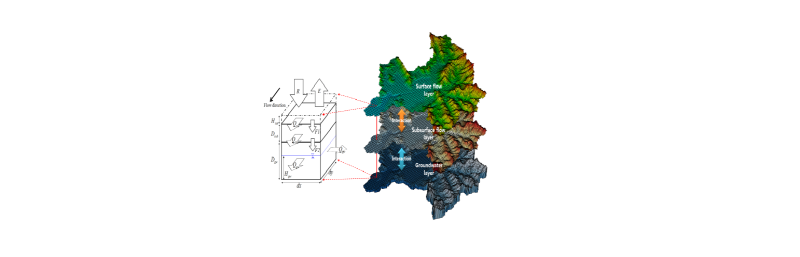
Fig. 1. Concept of water budget in a grid. R, rainfall; E, evapotranspiration; F1, infiltration from surface to subsurface layer; F2, infiltration from subsurface to ground water layer; Dsub, depth of subsurface layer; Dgw, depth of groundwater layer; Hsur, surface flow depth; Hgw, ground water depth; Qsur, discharge of surface layer; Qsub, discharge of subsurface layer; Qgw, discharge of groundwater layer; dx, dy, x- and y-direction cell size, respectively.
격자단위 물수지식의 구성에 있어서 몇 가지 가정을 전제하였다. 첫째, 지표유출은 격자의 흐름방향을 따라 한 방향으로만 흐른다. 둘째, 마찰경사는 바닥경사와 같다. 셋째, 강우 지속기간 동안에는 지하유출이 지표유출로 환원되지 않는다. 넷째, 침투는 수직방향으로만 이루어진다. 다섯째, 강우 시 증발산량은 미소하므로 고려하지 않는다.
지표흐름
본 연구에서 구성한 모형의 지표류층 물수지식은 다음과 같다.
(1)
여기서, A는 격자면적(m2), S는 지표류층의 저류량(m3), I와 Q는 주변격자와의 지표류 유입률(m3/s) 및 유출률(m3/s)이며, R은 강우강도(m/s), ET는 증발산량(m/s), F1은 지표면에서 토양으로의 침투량(m/s)이다. 지표면의 직접유출량에 기여하는 흐름은 지표흐름(surface flow)과 하천흐름(channel flow)으로 구별되고 일반적으로 천수방정식 형태의 연속방정식과 운동량방정식으로 해석이 가능하다. 지표류나 작은 하천흐름에서처럼 배수효과(backwater effect)가 없는 경우에는 운동량방정식의 동력학적인 항(dynamic term)을 무시하고 하도경사와 마찰경사를 같다고 가정하면 격자간의 표면유출량은 다음과 같은 식으로 표현하는 것이 가능하다.
(2)
여기서 Q는 유량(m3/s), A는 단면적(m2), R은 동수반경(m), n은 Manning의 조도계수이며, S0는 지표면경사 또는 하상경사(-)이다.
지표면의 증발산량은 다음식과 같이 Penman-Monteith 방법을 이용하여 산정하였다.
(3)
여기서, ET는 기준잠재증발산량(m/s), Rn은 지구/작물표면에서 순수하게 축적되는 에너지(MJm-2day-1), G는 토양 열 유속 밀도(soil heat flux density, MJm-2day-1), T는 2 m 높이에서 일평균기온(℃), u2는 2 m 높이에서 풍속(m/s), es는 포화증기압(kPa), ea는 실제증기압(kPa), es - ea는 포화증기압 결손량(kPa), Δ는 증기압 곡선의 기울기(kPa/℃), 그리고 γ는 건습계 상수(kPa/℃)이다.
표면에서 토양으로의 침투율은 다음식과 같이 Huggins and Monke (1968)가 제안한 토양함수량의 함수로 산정하였다.
(4)
여기서, FMAX는 침투율(mm/hr), fc는 종기침투율(mm/hr), Se는 토양의 포화율, fi는 초기침투율(mm/hr), b는 상수지수이며 본 연구에서는 선행연구를 참고하여 1.5를 사용하였다.
지표하 흐름
지표하 흐름층의 물수지 방정식은 다음과 같다.
(5)
여기서, Is와 Qs는 지표하 격자사이의 유입률과 유출률(m3/s), ηs는 지표하 토양수분층의 공극률(-), Hs는 지표하흐름층 수심(m), F2는 침루율(m/s)이다.
지표하 흐름의 이동방향은 Fig. 2에서와 같이 흐름누적도에 따라 8방향으로 결정되는 지표류의 흐름방향과 같으며 흐름률은 물수지(water balance)를 고려하여 다음식과 같이 계산하였다.
(6)
여기서, Qs는 지표하 흐름률(m3/s), Ds는 지표하 토양수분층 깊이(m)이다. 단, Hs가 Ds보다 작을 때는 지표하 흐름층이 포화되지 않은 상태로 지표하 흐름률은 발생하지 않는 것으로 가정하고 지표하 흐름률을 0으로 산정한다.
지표하 흐름층으로부터 지하수층으로의 침투는 지표하 흐름층이 포화되어 있을 때 (Hs > Ds), 그리고 지하수 수심이 지하수층의 깊이보다 작을 때 (Hgw < Dgw)라는 두 조건을 만족해야 하며 이때 침투율은 Darcy의 법칙에 의해 F2 = K와 같이 산정한다. 여기서 K는 투수계수(m/s)이다. 지하수 수심이 지하수층의 깊이보다 클 때 (Hgw > Dgw)는 반대로 지하수층에서 지표하흐름층으로의 침투가 발생하며 침투율은 지하수층의 물수지를 고려하여 다음식과 같이 산정한다.
(7)
여기서, Hgw는 지표수 수심(m), Dgw는 지하수층 깊이(m), ηgw는 지하수층의 공극률(-)이다.
지하수 흐름
지하수의 흐름은 2차원으로 고려하며 지하수 흐름의 연속방정식은 다음 식과 같다.
(8)
여기서, ugw, vgw는 x, y 방향의 지하수흐름 평균유속(m/s), Qw은 지하수 양수율(m3/s)로 양수를 하고 있는 격자에서만 유효한 값을 가지며 그 외 격자에서는 0의 값을 가진다.
지하수흐름 평균유속은 Darcy의 법칙에 따라 다음 식과 같이 산정된다.
(9)
여기서, Kgw는 지하수층의 투수계수(m/s)이다. 식(9)를 식(8)에 대입하면 다음과 같은 식을 얻을 수 있다.
(10)
위 편미분 방정식을 유한차분법(Finite Difference Method)로 이산화 하여 식을 정리하면 다음과 같은 관계식을 얻을 수 있다.
(11)
여기서, ∑Qgw는 옆 격자와의 지하수 흐름률의 합(m/s)이며, Hgwn는 옆 격자의 지하수 수심(m), ∆x는 격자 길이(m)이다.
Results and discussion
시험지역 및 자료
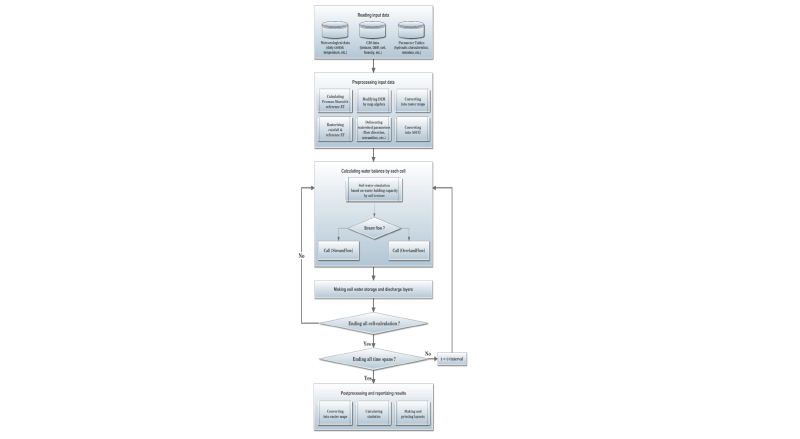
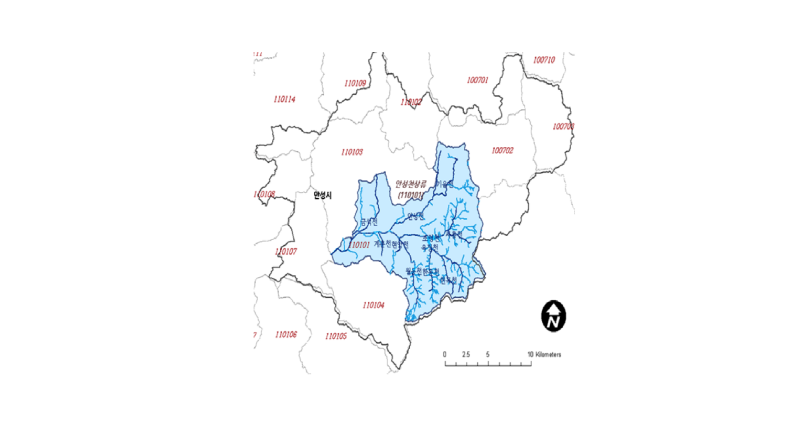
모형의 계산 Flow chart를 Fig. 4에 제시하였다. 모형의 시험지역으로 Fig. 5와 같은 안성천상류(표준유역코드 110101) 지역을 선정하였다. 시험지역은 안성천 수계에서 지방2급 하천인 조령천을 중심으로 안성천과 합류하는 수계로서 유역 내 소하천을 비롯한 총 연장이 약 192,964 m인 하천의 유역이다. 유역의 평균경사는 16.1%, 그리고 유역의 고도는 해발 10 m부터 해발 561 m까지 분포하고 있다. 유역내에 금광, 고삼, 마둔 저수지가 위치해 있어 안성천의 하천유량은 농번기 관개용수의 영향을 크게 받는다. 대상 유역은 산림지역이 약 47%로 가장 많이 분포하고 있으며 논과 밭을 포함한 농경지가 약 30%를 차지하고 있다.
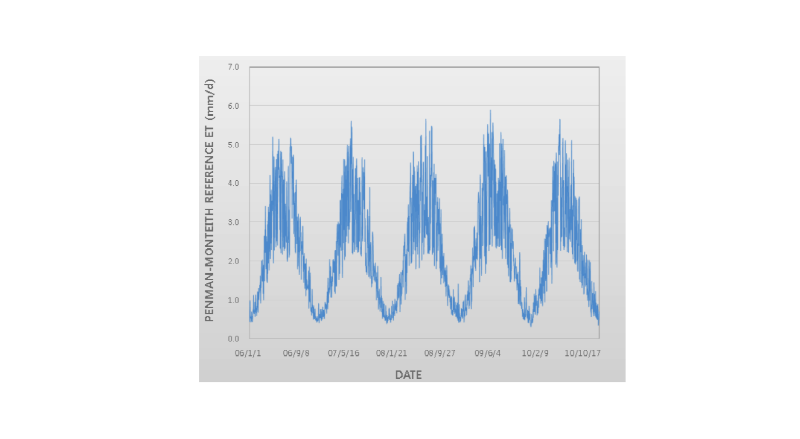
시험지역에 적용 가능한 기상청 기상관측소는 Thiessen망이 겹치는 이천(203)과 천안(232) 기상관측소가 있으며 안성시 보개면에 농업기상관측소가 1개소가 평균기온, 평균습도, 풍향, 풍속, 일조시간, 강수량 등을 관측하고 있다. 2001년 1월 1일부터 2015년까지 관측자료를 수집하여 정리하였으며, 수집된 기상자료를 바탕으로 일별 Penman-Monteith 기준증발산량을 계산하면 Fig. 6과 같다.
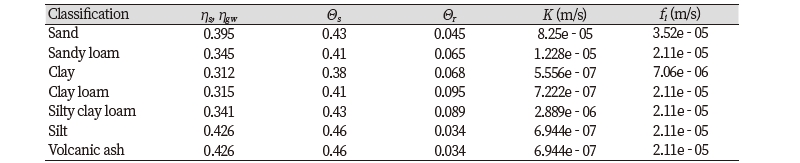
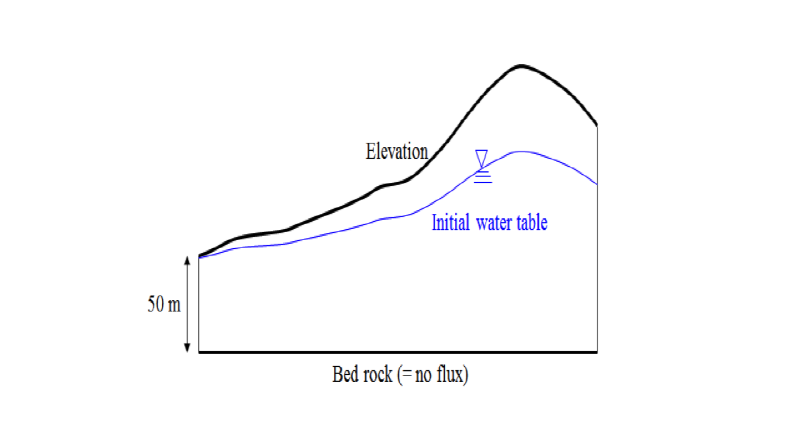
시험지역에 대하여 유역경계도(shp), 행정경계도(shp), 기상관측소위치도(shp), Thiessen망도(shp), 수치고도자료(grid), 중분류토지피복지도(shp), 정밀토양도(shp) 등의 수치지도를 확보하였고 이들 좌표체계를 국가표준좌표체계(GRS80)로 통일하여 사용하였다. 유효토심은 정밀토양도를 바탕으로 Table 1과 같이 산정하였다. 공극률, 투수계수, 초기침투량 등은 정밀토양도의 토성을 기준으로 Carsel and Perrish (1988)을 참고로 하여 Table 2와 같이 산정하였다. 종기침투율은 정밀토양도의 배수등급을 바탕으로 Natural Resources Conservation Service (NRCS)에서 제시한 토양군에 따른 침투율을 근거로 Table 3과 같이 산정하였다. Manning의 조도계수는 중분류 토지피복지도를 바탕으로 McCuen (1998)을 근거로 산정하였다. 초기 지하수심은 50 m + α × (Elevation - Elevation_outlet)과 같이 설정하여 자연스럽게 분포되도록 하였고 유역 출구에서 50 m가 되도록 하였다(Fig. 7). 단, 본 논문에서는α = 0.4로 설정하고 모의를 수행하였다.
|
Table 3. Evaluation of steady infiltration rate based on Natural Resources Conservation Service (NRCS) soil classification. 
|
|
|
fc, steady infiltration rate. |
|
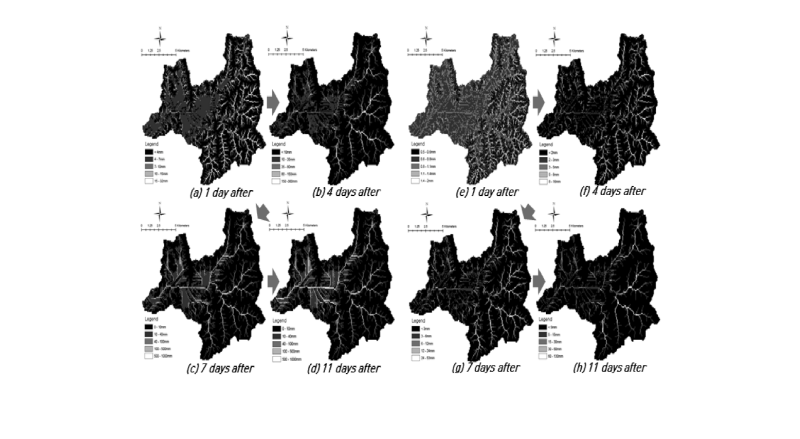
대상유역에 대하여 가상의 조건으로 시험모형의 구동을 시험하였다. 먼저 토양수분이동, 다양한 입력조건과 지하수 관정 시나리오 모듈의 적용 없이 단순 격자물수지 분석 시험을 수행하였다. 일정 기상조건으로 증발산량 5 mm/d, 침투량 10 mm/d, 강우지속일수 11일 조건에서 일강우량 20 mm/d인 경우와 50 mm/d인 경우를 모의 시험하였다. Fig. 8에서 확인할 수 있는 것과 같이 시간경과에 따라 다른 강우조건에서 격자별 저류량 누적값이 변화하는 것과 일강우량 조건의 차이를 확인할 수 있는 결과가 도출되었다.
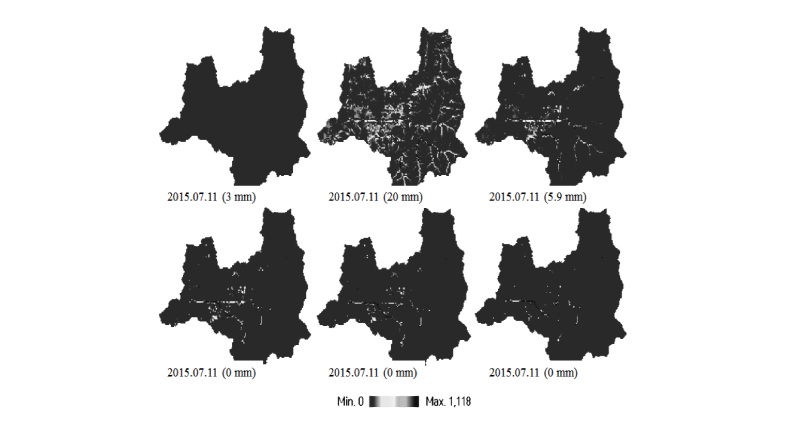
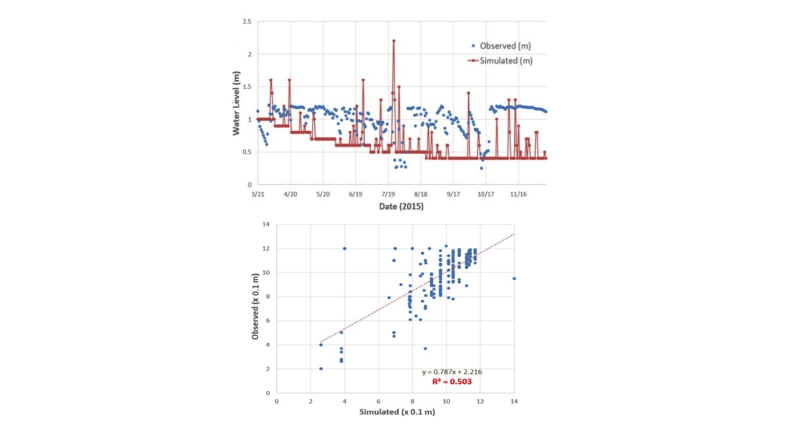
시험지역의 실 기상자료를 사용하여 Fig. 9과 같은 결과를 도출하였다. 그림에서 확인할 수 있듯이 일강우의 변화에 따라 지표흐름의 연속적인 변화를 확인할 수 있었다. 모형의 강우유출현상에 대한 성능을 검증하고자 대상유역의 하류에서의 수위를 비교하여 Fig. 10에 제시하였다. 제곱평균제곱근(root mean square)이 다소 낮은 0.5 수준으로 현재까지 모의결과로는 재현성이 높지 않은 것으로 보인다. 대상유역은 농업용 저수지가 하천의 유출량에 큰 영향을 미치는 지역이나 본 모형에서는 현재까지 농업용 저수지의 저류-방류를 고려하지 않고 있는 것이 정확도 낮은 주된 원인인 것으로 판단된다.
Conclusion
본 논문에서는 건천화 연구의 기초툴로서 사용될 수 있는 유역수문변화를 고려한 분포형 수문모델을 개발하였다. 본 연구에서 개발한 모형은 기존의 모형들에 대한 상세한 조사를 시초로 지표수흐름, 지표하흐름, 지하수흐름을 물리적으로 고려하도록 설계되었으며 지표수 수심, 토양수분량, 지하수 수위를 분석할 수 있도록 개발되었다. 또한 건천화의 원인이 되는 토지이용 변화, 지하수 취수 등의 현상을 종합적으로 고려할 수 있도록 설계되었다.
개발한 모형은 안성천 상류지역에 대하여 시험적용 되었으며 가상모의 및 실제 강우를 대상으로 한 모의에서 타당한 반응을 보였다. 하지만 실제수위와 모의수위를 비교할 때 다소 일치성이 낮은 결과를 보였으며 이는 개발한 모형에서 농업용 저수지의 저류-방류 상황을 반영하지 않았기 때문인 것으로 해석되었다. 따라서 향후 본 연구에서 개발한 모형의 보다 정확한 검증을 위해서 다수의 유역에 대하여 실제 유출량과의 비교가 필요할 것이며, 추가적인 매개변수의 동정에 관한 연구도 수행되어야 할 필요가 있다. 또한 건천화에 미치는 영향을 분석하기 위해서 관정과 토지이용변화에 대해서 추가적인 연구가 필요할 것이다.