Introduction
The tomato (Solanum lycopersicum) is one of the most important fruits in the world, with a total production that increased from 83.2 million ton in 1994 to 170.8 million ton in 2014 (FAOSTAT, 2017). It is considered healthy on account of its high lycopene content, which is a natural antioxidant, as well as β-carotene, vitamin C, and vitamin E (Rahman et al., 2017). Currently, consumers are willing to pay premium prices for a superior quality product. For tomatoes, this relates to a good appearance (e.g., color and size), desired texture (firmness), flavor (e.g., soluble solid content and acidity), and aroma (Huang et al., 2017). The surface color of the tomato changes with maturity, which also influences the texture and flavor.
In practical situations, tomato firmness is often used as the degree of ripeness for harvested fruits, which determines the postharvest quality and shelf life. However, heterogeneous fruit quality is encountered on account of the firmness variation of harvested fruits, which requires different postharvest handling procedures (Kienzle et al., 2012). Moreover, tomato flavor is dependent on the sugar and acid content. High sugars and relatively high acids are required for the best flavor. High acids and low sugars will produce a sour tomato, while high sugars and low acids will result in a tasteless tomato (Agbemavor et al., 2014). Thus, soluble solid content (SSC) and total titratable acidity (TA) are the main components that are responsible for the tomato flavor and properties that are most likely to align with the consumer perception of the internal quality. Therefore, it is necessary to measure these qualitative attributes from whole samples, which is very useful for producers, processors, and distributors to ascertain the quality of tomatoes. Currently, traditional analytical methods are used to analyze these qualitative attributes. These methods are costly and time-consuming as a result of the multiple steps needed and the use of hazardous reagents (Toledo-Martin et al., 2016; Lim et al., 2017). Moreover, traditional methods are destructive and consequently enable quality control to be performed only in a limited section of the fruit, rather than in the entire individual fruit (Lee et al., 2017; Lee et al., 2018).
In hyperspectral imaging (HSI), imaging and spectroscopy technologies are combined into a single system, thus simultaneously providing spectral and spatial information about a product (Ahmed et al., 2017; Qin et al., 2017). HSI shows considerable promise for non-destructive analysis of horticultural and food products, and it is ideally suited to the requirements of the agro-food industry in terms of quality control (Mo et al., 2017). To date, HSI has been used to measure the firmness of the apple (Noh and Lu, 2007; Mendoza et al., 2011; Wang et al., 2012; Zhu et al., 2013), peach (Lu and Peng, 2006), blueberry (Leiva-Valenzuela et al., 2013), strawberry (Tallada et al., 2006), banana (Rajkumar et al., 2012), kiwifruit (Zhu et al., 2017), tomato (Huang et al., 2017), and mango (Servakaranpalayam, 2006; Rungpichayapichet et al., 2017). Similar to firmness, the assessment of the acid and soluble solid content (SSC) has also been conducted using the HSI systems for fruits such as the apple (Noh and Lu, 2007; Mendoza et al., 2011; Zhu et al., 2013), kiwifruit (Guo et al., 2016), banana (Rajkumar et al., 2012), strawberry (ElMasry et al., 2007), blueberry (Leiva-Valenzuela et al., 2013), tomato (Huang et al., 2017; Rahman et al., 2017), bell pepper (Schmilovitch et al., 2014), and grape (Baiano et al., 2012; Nogales-Bueno et al., 2014).
Most studies have used HSI systems with the scatter mode for firmness, SSC, and acidity determination. Therefore, the prediction results of fruit firmness, SSC, or acidity must be improved because the hyperspectral scattering images contain a considerable amount of redundant information in hundreds of spectral wavelengths. Moreover, minimal attention has been paid to determining the firmness, SSC, and acidity based on a variable selection method and robust calibration models. The short-wave infrared (IR) region (750 and 1900 nm) in the electromagnetic spectrum is associated with the vibration and combination overtones of O-H, C-H, and N-H bonds, which are the primary structural components of organic molecules (Williams and Norris, 2001). Thus, the application of HSI in the spectral range of 1000 - 1600 nm has potential to predict the firmness and sweetness index (SI; ratio of TA and SSC) in tomatoes using a variable selection method. Therefore, the objectives of the present study are to examine the feasibility of predicting the firmness and SI of tomatoes using HSI, and to establish calibration models based on a variable selection method that enables the quality of tomatoes to be predicted in a non-destructive manner.
Material and Methods
Tomato samples
A total of 95 fresh, fully matured tomatoes that were uniform in size and color, and were free from damage, were purchased from a local supermarket in Daejeon city, Republic of Korea. These tomato samples weighed 102 ± 12 g on average and measured an average of 60 ± 3 cm in length on the major axis, and 50 ± 4 cm in width on the minor axis. All samples were stored in a refrigerator at 10°C and 85% RH until the experiments were conducted. Prior to the experiment, the tomato samples were moved from the refrigerator to a laboratory with an ambient temperature of 20°C and held there for 4 h to avoid any potential cross-effects arising from the storage temperature on the measurements.
Hyperspectral image system
The tomato images were acquired in the reflectance mode using a push-broom HSI system with a diffuse lighting system, as described by Rahman et al. (2017). The system consisted of a line-scan image spectrograph (Headwall Photonics, Fitchburg, MA, USA) that covered the spectral range of 1000 - 2500 nm with a 7.5-nm spectral resolution, mercury cadmium telluride (MCT) detectors to detect the radiation reflected back from the samples, and a high-performance camera with a detector with a size of 320 × 256 pixels (Headwall Photonics, Fitchburg, MA, USA). It also included a 1.4/25 C-mount lens (Navitar, Inc., Rochester, NY, USA), translation stage, and computer-supported with image acquisition software for controlling the camera and acquiring images. The tomato samples were illuminated with a diffused light provided by four tungsten-halogen (Light Bank, Ushio Inc., Tokyo, Japan) light sources with fiber optics (each 100 W, 12 V) that were located at the circumference of a diffusing dome at equal distances from one another. The samples were randomly placed on a sample stage 40 cm from the HSI system and the image was acquired by scanning each sample line by line as it moved through the system.
Image calibration
The raw hyperspectral images were calibrated to obtain relative reflectance images to remove the noise generated by the device and the effects of uneven light-source intensities. To calibrate the raw images, a white (W) reference image with approximately 100% reflectance and a dark (D) reference image with approximately 0% reflectance were captured. The white reference image was acquired from a white Teflon calibration tile under the same condition asthe raw image, while the dark reference image was obtained by turning off the light source along with completely closing the lens of the camera with its opaque cap. These reference images, W and D, were then used to convert raw reflectance images (R0) to relative reflectance images (R)—which are also known as calibrated hyperspectral or corrected images—according to the following equation:
(1)
The corrected images were used as the basis for subsequent analysis to extract spectral information and for effective wavelength selection, prediction, and visualization purposes.
Extraction of spectral data
The calibrated hyperspectral image was segmented by using a simple threshold value as the average value of the background and tomato pixels to remove the background effect and visualize only the tomato pixels. Then, the reflectance spectrum from the six different parts of the tomato image using a 10 × 10 pixel square area was computed by averaging the spectral value of all six parts. Accordingly, only one mean spectrum was produced for each sample, given that the reference firmness and SI values from the laboratory analysis produced only one value per sample, which was the average over the entire sample. The same routines were repeated for all tested samples; thus, a total of 95 mean reflectance spectra, representing 95 analyzed tomato samples, were extracted and saved, respectively. Owing to the low signal-to-noise (S/N) ratio performance stemming from the inefficiencies of the lighting system at certain wavelength regions, e.g., the low light output above 1550 nm, the spectra were limited to the 1000 - 1550 nm range, which the relative intensity is greater than 0.05. Background segmentation and extraction of spectral data from the hyperspectral images were programmed using MATLAB software (version 8, MathWorks Inc., Natick, MA, USA).
Reference analyses of quality attributes
After image acquisition, the firmness and SI of each sample were measured. The firmness of the tomato was measured using a Universal Instron Texturometer (Model 3343, single-column, Instron Corp., Norwood, MA, USA) to perform puncture tests using a 10 mm diameter flat-face probe and a 500 N load cell at a speed of 10 mm/min. The measurements were performed in the equatorial region for each fruit. The maximum force (N) was recorded to penetrate the tomato and was attributed to the fruit firmness.
Immediately after conducting the firmness measurements, each tomato fruit was juiced by using a manual stainless-steel squeezer, and the resultant tomato juice was filtered through a 250 µm metallic sieve. The SI was determined by the following procedures outlined by Agbemavor et al. (2014) and expressed according to the following relation:
(2)
The SSC of each tomato was measured using a digital refractometer (model: PR-32α; Atago Co., Tokyo, Japan) with a scale of 0 - 32% Brix (lowest count = 0.1% Brix) at room temperature (~ 22°C). Approximately 1 mL of the fruit filtrate (juice) was applied to the loading point of the refractometer and the %Brix reading was directly obtained from the scale.
The titratable acidity (TA) content was determined according to the method reported by Saad et al. (2016). Approximately 10 g of juice was diluted in 50 mL of distilled water and titrated against 0.1 N sodium hydroxide (NaOH) in the presence of three drops of phenolphthalein until a pH of 8.2 (pink) was attained. The TA content as a percentage of citric acid was estimated using the following relation:
(3)
where T is the amount of NaOH needed to attain pH of 8.2 (mL), C is the milliequivalent weight of citric acid (0.064), N is the normality of NaOH (0.1), and J is the amount of juice (g).
Data analysis
Spectral preprocessing
In spectral analysis, various preprocessing techniques are often applied to correct the undesired effects or errors that are not associated with the studied responses. In this study, several types of mathematical pretreatment techniques were separately employed before calibration modeling to select the optimum technique for the dataset correction, namely normalization (mean, maximum, and range normalization), multiple scatter correction (MSC), standard normal vitiate (SNV), and Savitzky–Golay (first and second derivative). Normalization is a preprocessing technique that is most often used to eliminate the scattering effect in the spectra (Rahman et al., 2017). The MSC method is well suited to correct the scattering level of the spectra by eliminating the spectral difference of the data (Kandpal et al., 2015). SNV is another spectra correction method that removes the slope variation from the spectra generated by the scattering (Barnes et al., 1989; Candolfi et al., 1999). Moreover, thederivative technique has been intensively used to remove baseline shift and super-imposed peaks (Rahman et al., 2015). In this study, after preprocessing of the spectra, the samples were divided into two sets using the Kennard–Stone (KS) sampling algorithm (Kennard and Stone, 1969). A calibration sample set, consisting of 60 samples was used to develop the calibration model, and a prediction sample set consisting of 35 samples was used for prediction purposes.
Partial least squares regression model
Partial least squares (PLS) regression is the most common multivariate method for constructing calibration models to determine the constituent of interest. It is very efficient for multivariate calibration when the measured variables, such as the spectral data, are numerous and highly correlated (Kamruzzaman et al., 2012a). In this study, the preprocessed spectral data were linked to the firmness and SI of tomatoes using a PLS regression analysis to develop a calibration model. In the development of all the calibration and prediction models, 20 PLS factors were set as the maximums. The performances of the developed models were evaluated using several statistical parameters, including the standard error of calibration (SEC), coefficient of correlation for calibration (Rcal), standard error of the prediction estimate (SEP), coefficient of correlation for prediction (Rpred), and number of latent variables. Generally, a good model should have a high coefficient of correlation (R) and a low SEP. In addition, the difference between SEC and SEP is an indicator for evaluatinga good calibration model (Rahman et al., 2016). Another important parameter is the number of latent variables that are used to explain the complexity of the model (Rahman et al., 2015).
Feature wavelength selection
Because of the high spectral resolution of HSI systems, hyperspectral images usually contain an immense amount of spectral data, resulting in a large number of wavelength variables. In principle, selecting the characteristic wavelengths and eliminating uninformative ones can produce better and simpler prediction models. Indeed, the removal of redundant, irrelevant, and noisy wavelengths can typically enhance the models in terms of accuracy and robustness, while also reducing their complexity (Kamruzzaman et al., 2013; Kandpal et al., 2016; Zhu et al., 2016). In this study, the variable importance in projection (VIP) was applied to the best-preprocessed calibration data set to select the optimum wavelengths for evaluating the firmness and SI of tomatoes using the minimum number of wavebands. The VIP score for the j-th variable can be defined as:
(4)
where VIP is the variable importance for the projection (dimensionless), j denotes a specific wavelength (nm), P is the number of wavelengths (dimensionless), h is the number of latent variables (dimensionless), Z is the fraction of variance in the prediction explained by the latent variable (dimensionless), and W is the loading weight (dimensionless).
The VIP score verifies the impacts of the various wavelengths on predictions. More specifically, the higher the VIP score is, the more important is the response variable as a predictor. The variables with VIP scores greater than 1.0 are highly influential; those with VIP scores lower than 0.8 are insignificant as predictors (Wold et al., 2001; Steidle Neto et al., 2017). Finally, a PLS regression model was developed for predicting firmness and SI content on the basis of the VIP scores using these feature wavelengths.
Image visualization and prediction map
Prediction maps of firmness and SI were generated using tomato halves from the equatorial axis for showing internal composition by applying weighted regression beta coefficients (BW) yielded by the PLS-VIP regression model to each pixel with its own corresponding spectrum. The prediction result of each pixel was displayed and plotted according to the constituent of the sample based on its spectral signature to provide the distribution gradient in the sample (Rungpichayapichet et al., 2017). The spatial distributions of firmness and SI were illustrated by color gradients, which were used to depict the respective values in the fruit samples. The following equation can be used to develop the prediction map:
(5)
where Ii is the i-th image of n reflectance spectral images, Ri is the BW derived from the PLS–VIP regression model, and C is the constant of the PLS–VIP regression model. All image-processing steps required for visualization purposes were performed using MATLAB software (version 8, MathWorks, Inc., MA, USA).
Results and Discussion
Spectral profile characteristics
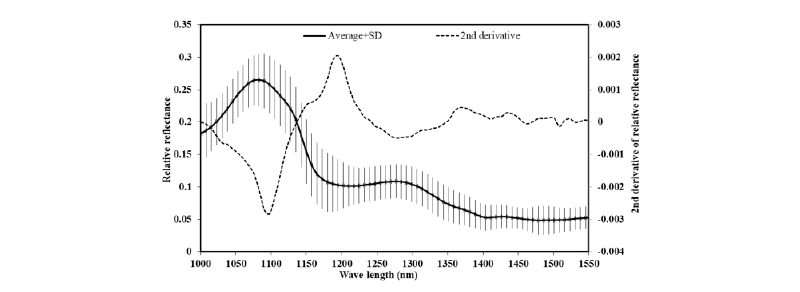
Fig. 1 shows the average relative reflectance spectra and standard deviation (SD) with the resulting second-derivative spectral profile at the spectral range of 1000 - 1550 nm using 74 bands (variables), which is similar to previous studies (He et al., 2005; Rahman et al., 2017). These spectra regions were sensitive to the concentrations of organic materials, which involved the responses of molecular bonds C-H, O-H, and N-H. The water content contained the bond O-H, which is responsible for fruit firmness. In the spectra, the absorption features (valleys) are observed at around 1190 nm and 1450 nm, corresponding to the absorption maxima of water (Penchaiya et al., 2009). Moreover, the SI is the product of SSC and TA of fruits and also contains bonds C-H, C-O, and C-C. However, their absorption peaks overlap in several parts of the spectral region.
In Fig. 1, it is observed that the absorption peak at 1190 nm is likely attributed to the C-H stretching the second overtone from fructose, sucrose, and glucose (Guo et al., 2016). In addition, the small absorbance trend at 1350 - 1500 nm maybe associated with sucrose, fructose, and glucose in fruit. However, these reflection peaks are usually located in the wide spectral band. Therefore, those key wavelengths that are helpful to predict firmness and the SI of tomatoes cannot be directly identified.
Statistics of measured samples
The descriptive statistics for the quality attributes (firmness and SI) determined by the standard methods of the two sample sets are summarized in Table 1. A relatively high variability covering a large scope was anticipated in firmness, which was beneficial to developing a robust calibration model. It may be assumed that the moisture content variation among the samples resulted in the difference in firmness. Nevertheless, the measured SI of tomatoes showed the smallest variation with a considerable range, which was likely a consequence of the naturally low levels of organic acids in tomatoes.
|
Table 1. Statistics of quality parameters for tomato measured by standard methods. 
|
|
|
SI, sweetness index; a.u., arbitrary unit. |
|
PLS regression models using full spectra
The PLS regression for prediction of firmness and SI are summarized in Table 2. A good regression correlation coefficient using different preprocessing methods was obtained in the calibration set, with Rcal ranging from 0.90 to 0.93 (SEC = 0.57 to 0.69 N) for firmness and Rcal from 0.81 to 0.86 (SEC = 0.29 to 0.33) for SI, respectively. When the model was used to predict the samples, the performances showed that the values of Rpred with different preprocessing methods varied from 0.62 to 0.82 for firmness and from 0.31 to 0.74 for SI content in tomatoes. The relatively low correlation coefficients for SI prediction could be attributed to the lack of variations in the SI among the tomato samples.
As shown in Table 2, the firmness and SI have better results for the Savitzky–Golay second-derivative preprocessing method, with Rpred = 0.86 (SEP = 0.86 N) for the firmness parameter and Rpred = 0.74 (SEP = 0.63) for SI, which is consistent with the results obtained in previous studies (Camps et al., 2012; Huang et al., 2017; Rahman et al., 2017). Specifically, the PLS regression model appears to be acceptable on account of only eight factors (LVs) for firmness and the three factors (LVs) for SI that were used in the calibration model.
Selection of the feature wavelengths
It was necessary to reduce the wavelengths owing to the computational burden and to speed up the prediction and visualization process. In fact, the wavelength reduction is especially desirable for the development of simple imaging systems for real-time applications. The reduced number of wavelengths can help decrease the time required to acquire and process each hyperspectral image (Kamruzzaman et al., 2012b). In the present study, the VIP scores resulting from the best preprocessing PLS regression model were used to develop a robust model by selection of feature-related wavelengths for firmness and SI of tomatoes. The VIP scores indicated the significance of specific wavelengths for the firmness and SI content of the samples. The performance of the developed model by PLS regression depended largely on the cut-off value of the VIP scores. Generally, the “greater-than-one” rule is used to select the feature wavelengths (Andersen and Bro, 2010). In this study, we chose a cut-off value of one, i.e., the number of selected wavelengths for the PLS model given that the maximum allowable number is one (Fig. 2). Because one objective of this work was to minimize the number of wavelengths as much as possible, a cutoff value of onewas used, and 18 and 24 optimal wavebands were selected from all 74 wavebands for the firmness and SI of the tomatoes, respectively.
In Fig. 2(a), it is observed that the most intensive absorption occurs around 1050 - 1150 nm, a region that relates to the first O-H stretching overtone (Büning-Pfaue, 2003). It is often applied in the quantitative analysis of high water content in fruits, the latter of which is responsible for fruit firmness. SI represents the content of organic molecules and is thus associated with the peaks arising from bonds, such as C-H, O-H, C-O, and C-C. Fig. 2(b) shows the apparent strong absorption peaks at 1050 - 1150 nm and - 1450 nm, which are associated with a combination of the second overtone of C-H stretching, the first overtone of -OH of the carboxylic acid group (Dong et al., 2013) and overtones of O-H stretching in H2O, respectively (Liu et al., 2010). Moreover, other detected specific absorptions relate to -CH=CH- bonds, with peaks observed between 1090 and 1120 nm, as shown in Fig. 2(b) (Su and Sun, 2016). Thus, we may conclude that the model developed using these selected wavelengths should be more robust and efficient for predicting the firmness and SI content of tomatoes.
PLS regression model using feature wavelengths
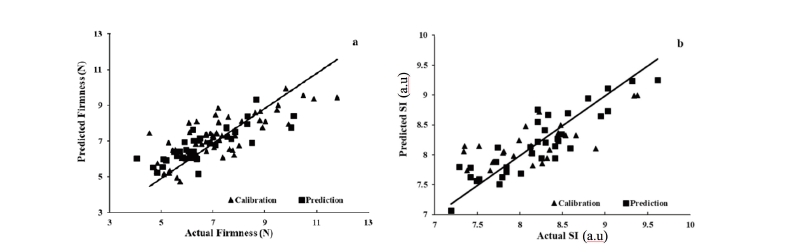
As a consequence of the previous analyses, the selection of feature wavelengths prominently reduced the number of wavelengths. The selected wavelengths were then applied to establish the calibration models instead of the full spectra using PLS regression. To accurately predict the firmness and SI of tomatoes and acquire more information, we applied the best preprocessing method (S-G second derivatives) for developing the PLS regression model. The selected feature wavelengths are displayed in Fig. 3. In these scatter plots, the ordinate and abscissa axes represent the predicted and measured fitted values of the corresponding parameters. The model shows very satisfactory behavior in terms of the correlation between the measured and predicted firmness and SI contents of tomatoes.
The PLS regression model was developed using the selected wavelengths (PLS-VIP), and the results using full wavelengths are given in Table 3. As shown in Table 3, the performance of the PLS regression model developed using the selected wavelengths for firmness prediction is slightly degraded (Rpred, 0.76 versus 0.82; SEP, 1.01 N versus 0.86 N) compared to the model developed using full wavelengths. However, the number of variables is reduced by 75.68% (from 74 to 18) and the number of latent variables is also reduced (from 8 to 4), which helps to minimize the complexity of the model. In the case of SI prediction, the model developed using the selected variables shows good performance compared to that developed using the full spectral range of 74 variables. The PLS regression model developed using selected wavelengths (PLS-VIP) predicts the SI content of tomatoes with Rpred of 0.81, SEP of 0.33, and the number of latent variables of two. These values are 0.74, 0.63, and 3, respectively, using the full-range spectra. It is evident that the performance of the PLS-VIP model is comparable to that of the model developed with the full spectra, even though 67.6% of the variables are eliminated. These results demonstrate that a calibration model for the prediction of firmness and SI content of tomatoes based on HSI was successfully developed and validated.
Visualization of quality attributes
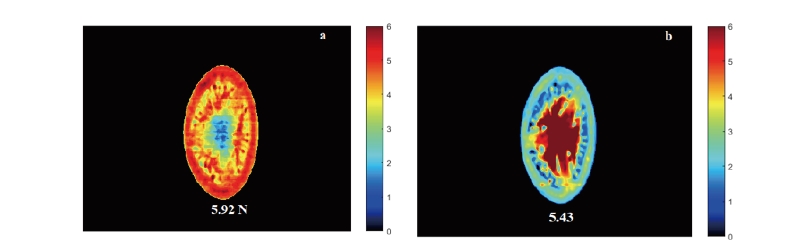
The above-described results of modeling were all based on the averaged spectra of each intact tomato hyperspectral image. It is known that each pixel in the hyperspectral image has its own spectrum, and this spectrum of an individual pixel in a sample can be used to visualize the chemical constituents. In this study, the BWs obtained from the PLS regression model developed using selected wavelengths were applied to each pixel in a tomato-halve image from the equatorial axis for visualizing the tomato firmness and SI content. In Fig. 4 shows the prediction maps of firmness and SI content, where different colors correspond to different levels of firmness, as well as the SI content in the sample, which is proportional to the spectral differences of the individual pixels.
The usefulness of these prediction maps is demonstrated by their capacity to provide rapid and easy access to the spatial distributions of firmness and SI content, whereby the relative concentrations are indicated by the color bars. It is shown in Fig. 4 that the firmness of the tomato shows a higher distribution along the peripheral area of the fruit, while it is lower in the middle part. In the case of SI content, the lower SI shows a uniform distribution in the tomato periphery and a greater SI towards the central part. The differences in the tomato quality, such as the firmness and SI content, may be caused by the differences in the exposure of the fruit surface to sunlight during cultivation. The distribution maps obtained in this study demonstrate the advantages of HSI that cannot be achieved with either conventional imaging or conventional spectroscopy alone.
Conclusions
The feasibility of using HSI techniques in the spectral region of 1000 - 1550 nm for predicting the firmness and SI content of tomato fruits using selected feature wavelengths was established in this study. A PLS regression model with different preprocessing techniques was developed for the entire spectral range and showed reasonable performance for predicting tomato firmness and SI content. The results showed that the firmness and SI contenthad better results for the Savitzky–Golay second-derivative preprocessing method, with Rpred = 0.86 (SEP = 0.86 N) and Rpred = 0.74 (SEP = 0.63), respectively. The VIP scores were used to select the feature wavelengths associated with the corresponding firmness and SI content. The PLS model developed based on feature wavelengths yielded Rpred of 0.76 and 0.81, with SEP of 1.01 N and 0.33 for firmness and SI content, respectively. Finally, chemical images were created to visualize the individual quality components of the tomatoes in a pixel-wise manner that cannot be obtained with either imaging or conventional spectroscopy. Based on the current results, HSI can be considered a potential technique for non-destructive grading of tomatoes based on firmness and SI qualities. In the future, additional cultivars with differing shapes, colors, and growing conditions will be examined to develop more robust regression models.