Sequential sampling method for monitoring potato tuber moths (Phthorimaea operculella) in potato fields

ENGINEERING

Sequential sampling method for monitoring potato tuber moths (Phthorimaea operculella) in potato fields

Jae-Min Jung¹

, Dae-hyeon Byeon¹

, Eunji Kim²

, Hye-Min Byun ²

, Jaekook Park ²

, Jihoon Kim³

, Jongmin Bae ²

, Kyutae Kim²

, Roca-Cusachs Marcos ³

, Minjoon Kang ²

, Subin Choi ³

, Sumin Oh ³

, Sunghoon Jung ^2,3

, Wang-Hee Lee ^1,2^*

¹Department of Biosystems Machinery Engineering, Chungnam National University, Daejeon 34134, Korea

²Department of Smart Agriculture Systems, Chungnam National University, Daejeon 34134, Korea

³Department of Applied Biology, Chungnam National University, Daejeon 34134, Korea

47(3):615 -624
Received Date: 26 March 2020
Revised Date: 31 July 2020
Accepted Date: 03 August 2020
DOI: 10.7744/kjoas.20200049
Check for Update!
Cited by
Citation

Abstract

An effective sampling method is necessary to monitor potato tuber moths (Phthorimaea operculella) because they are the biggest concern in potato-cultivating areas. In this study, a sequential sampling method was developed based on the results of field surveys of potato tuber moths in South Korea. Potato tuber moths were collected in fields cultivating potatoes at six sites, and their spatial distribution was investigated using the Taylor power law. The optimal sampling size and cumulative number of potato tuber moths in traps to stop sampling were determined based on the spatial distribution pattern and mean density of the collected potato tuber moths. Finally, the developed sampling method was applied to propose a control action, and its sampling efficiency was compared with that of the traditional sampling method using a binomial distribution. The potato tuber moths tended to aggregate; the optimal number was approximately 5 - 16 traps for sampling, and the number varied with the mean density of potato tuber moths according to the sampling sites. In addition, one, two, and three sites might require the following actions: Continued sampling, control, and no control, respectively. Sampling with the binomial distribution showed the minimum sample size was 12 when considering the economic threshold level. Here, we propose an effective sampling method that can be applied for future monitoring and field surveys of potato tuber moths in South Korea.

Keyword

control decision, field collection, potato tuber moth, sample number, sequential sampling method

Introduction

Potato tuber moth (Phthorimaea operculella) is the most significant pest in potato cultivation and storage, causing damage in over 100 countries (Kroschel et al., 2013). In addition, changes in moth distribution owing to climate change are a concern in major potato-producing countries (Jung et al., 2020). For example, the annual economic loss is estimated to be up to 70% in India, the Middle East, North Africa, and South America (Saxena and Rizvi, 1974; Raman and Palacios, 1982; Abewoy, 2018). The ability of the moth to adapt to a new environment has resulted in its introduction into South Korea and its population expanding throughout the country (Maharjan and Jung, 2011; Kwon et al., 2017). Therefore, intensive sampling and monitoring to prevent outbreaks are necessary.

Sampling is the first step in pest distribution and epidemiological investigations. However, field surveys to collect samples of pests is intensive in terms of time, cost, and labor; thus, an effective sampling method has been designed by a model-based approach as it computationally predicts outcomes in advance (Kim et al., 2016). As an effective approach, a sequential sampling method has been developed. It determines the size of samples and number of pests to stop sampling based on the spatial distribution pattern in the sampling site and the number of collected individuals (Kuno, 1969; Green, 1970; Iwao, 1975). In addition, it can help estimate the number of collected pests to determine whether control actions should be taken. Consequently, this method can assist in more efficient and precise sampling (Song et al., 2015); thus, it has been used for various target species including Plutella xylostella (Hamilton et al., 2004), Schizaphis graminum, (Giles et al., 2000), Bactericera cockerelli (Butler and Trumble, 2012), Tuta absoluta (Cocco et al., 2015), and Colias lesbia (Serra et al., 2013) in a greenhouse or field. In South Korea, the sequential sampling method has been used to develop an effective sampling strategy and to suggest actions for controlling Bemisia tabaci (Choi and Park, 2015) and Tetranychus urticae (Choe et al., 2017) in greenhouses. In addition, bacterial leaf blight-infected garlic was sampled using a sequential sampling method to determine the number of samples and the spot for sampling (Song et al., 2015). For insects affecting stored products, the sequential sampling method has been applied to evaluate the density of Sitophilus zeamais and Plodia interpunctella in rice storage (Nam et al., 2009).

Although the sequential sampling method has been applied to study a few notable pests, it has never been applied for potato tuber moths, and its application in field surveys is limited in South Korea. In addition, a previous study investigated the domestic distribution of potato tuber moths, but it did not use the sequential sampling method (Kwon et al., 2017). Therefore, it is necessary to develop an effective sampling method for monitoring potato tuber moth, which is the biggest concern in potato cultivation in South Korea. The objective of this study was to develop a sequential sampling method for field monitoring and controlling potato tuber moths. Based on the field survey results, we analyzed the spatial distribution of potato tuber moths and developed a sequential sampling method to estimate the optimal number of samples and potato tuber moths per sample effective for monitoring potato tuber moths. In addition, a control decision line was proposed based on the cumulative number of potato tuber moths in the sample and the sample size determined using the conventional statistical method.

Materials and Methods

Sample collection

Field surveys were carried out for 10 months. Potato tuber moths were collected using sex pheromone sticky traps (Delta trap: 275 mm × 195 mm × 170 mm; sticky trap: 235 mm × 190 mm; lure: 20 mm × 10 mm) (Green Agro Tech Co., Ltd., Gyeongsan, Korea) in six potato-cultivating arable lands in South Korea (mainland: Goryeong-gun, Miryang-gun, Sangju-si, and Uiryeong-gun; and the Island of Jeju: Jeju-si and Seogwipo-si) from March to November in 2019. Three traps were installed per farmland. The traps were changed every month, and the moths collected were counted. The moth vouchers have been deposited in the Laboratory of Systematic Entomology, Chungnam National University (Daejeon, Korea).

Spatial distribution analysis

A sequential sampling method using Green’s (1970) method can be established based on the spatial distribution pattern of moths in the field (Hamilton and Hepworth, 2004). To analyze the spatial distribution pattern of potato tuber moths in the field, the Tylor power law (TPL) has been applied (Taylor, 1961; Taylor, 1965). The TPL was used to estimate the spatial distribution of the species population based on the relationship between the mean and variance of the collected sample (Equation 1) (Taylor, 1961; Choe et al., 2017):

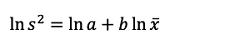(1)

where, and s are the mean density and variance of the trapped population, respectively, and a and b are the estimated parameters of slope and intercept, respectively. In this analysis, a is related to the sampling environment, such as labor and field size, and b is the Taylor’s aggregation index (Cocco et al., 2015). If the value of b is not significantly different from 1, the distribution is random, whereas b > 1 or b < 1 means that the distribution is aggregated or uniform, respectively (Southwood, 1978; Hamilton and Hepworth, 2004).

Development of a sequential sampling method

To develop a sequential sampling method, we initially estimated the optimal sampling size for Green’s (1970) method using the method proposed by Karandinos (1976) (Equation 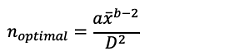2):

(2)

where, a and b are regression parameters obtained from TPL, D is the desired level of precision, and is the mean density.

Then, stop lines for sequential sampling of potato tuber moths were calculated based on the parameters estimated from the TPL (Green, 1970) (Equation 3):

(3)

where, Tn is the cumulative number of potato tuber moths sampled, a and b are regression parameters obtained from TPL, D is the desired level of precision, and n is the total number of samples.

The optimal sampling size was then plotted against the mean density of potato tuber moths according to the desired level of precision. Previous studies suggested that D of 0.1 is the usual value for research purposes, while 0.2 or 0.3 would be practically plausible for pest sampling (Southwood, 1978; Manly, 1989; Hamilton and Hepworth, 2004). For this reason, we set the D value as 0.1, 0.2, and 0.3. In addition, a sequential sampling chart with a stop line was constructed by plotting Tn against the number of traps to be sampled.

Establishing a control decision line

To determine the number of potato tuber moths at which a control method is required, we used a previously suggested method (Iwao, 1975; Wise and Lamb, 1995; Choe et al., 2017) (Equation 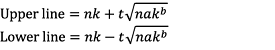4):

(4)

where, n is the number of samples, k is the value of economic damage tolerance at the density of pests requiring control, a and b are regression parameters obtained from the TPL, and t is the value of t-statistics at a specific significance level.

In this study, we used 15 and 20 for k, because 15 - 20 moths per trap per night is the recommended economic threshold level at which insecticide application is required to reduce yield damage of potato (Rondon, 2010; Abewoy, 2018), and plotted both lines against the number of samples at t = 2.35 at the significance level of 0.05 (Choi and Park, 2015).

In the plot, the cumulative number of potato tuber moths collected from traps above the upper line indicates the necessity for a control action, whereas a value below the lower line indicates that no action is required. When the cumulative number of potato tuber moths is between the upper and lower lines, continuous sampling to make a control decision is necessary.

Estimating sample size using binomial distribution

The probability function was employed as a comparable traditional method with a sequential sampling method for determining sample size, that is, number of traps in this study. Binomial distribution is a popular statistical approach applied for estimating sample size, because it can be used to calculate the probability of an event occurring independently and repeatedly (Kim et al., 2019, 2020). By modifying the formula of binomial distribution, we calculated the probability of at least one potato tuber moth trapped with m number of traps:

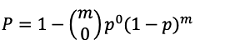(5)

where, m is the number of traps and p is the ratio of the distribution of potato tuber moth to the total field area.

In this study, p was considered the ratio of potato tuber moth, which causes damage to potato cultivation and requires control measures. Hence, p was set to be 0.16 and 0.22, because the calculated economic threshold level has been shown to range from 15.7% to 21.5% (Abdallah, 2017). The significance level was set at 0.05. With these values, we changed the number of samples until the probability of detecting at least one individual potato tuber moth reached a 95% confidence level.

Software

SAS software package (version 9.4, SAS Institute Inc., Cary, NC, USA) and MATLAB (2019a, The Mathworks, Inc., Natick, MA, USA) were used for regression analysis and probability calculation, respectively. All plots were generated using SigmaPlot (version 12.5, Systat Software Inc., San Jose, CA, USA) and the map showing the cities where field surveys were conducted was constructed using ArcGIS (version 10.4.1, ESRI, Redlands, CA, USA).

Results and Discussion

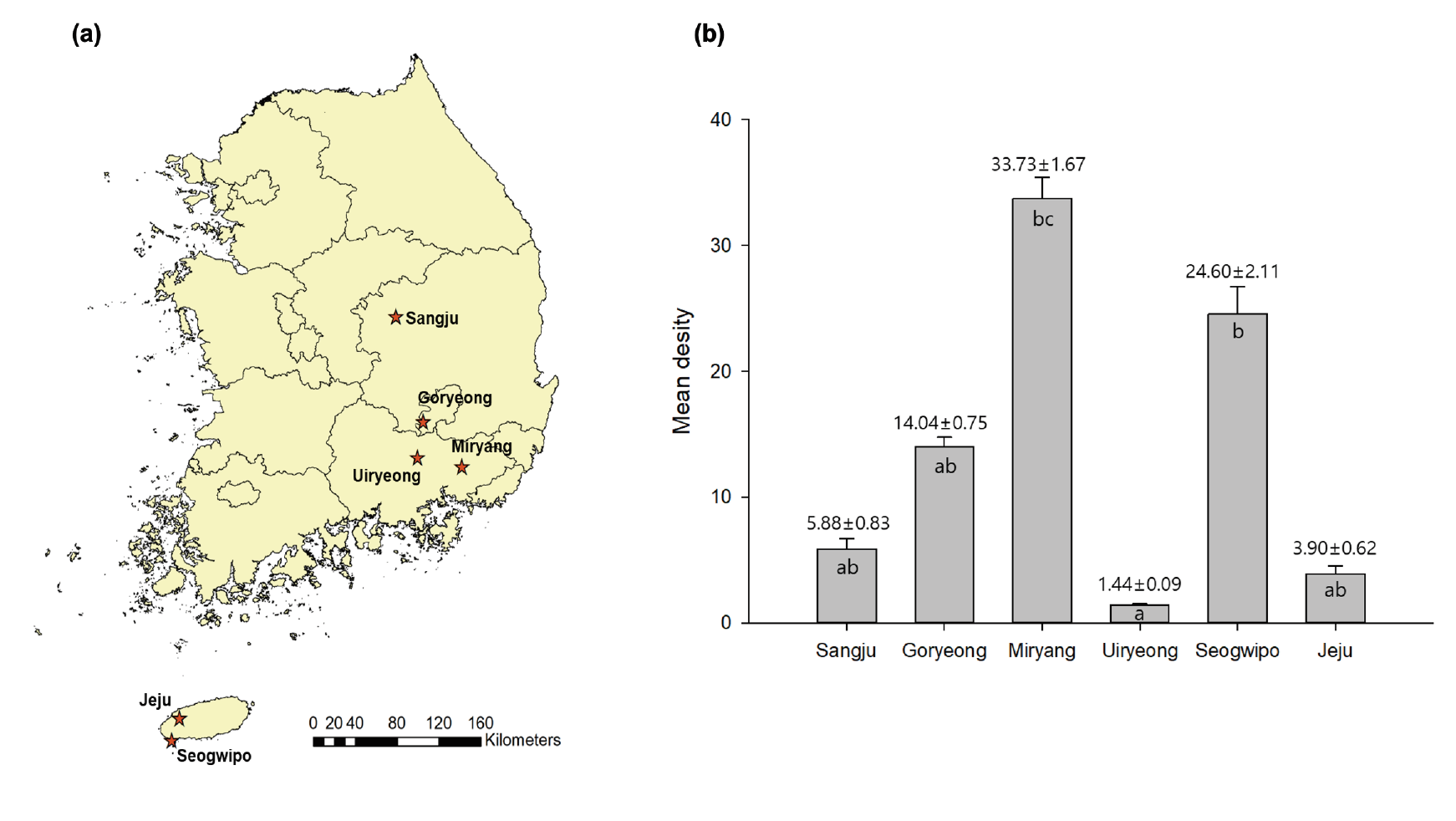
Field surveys of potato tuber moths were conducted in six cities, which are marked in the map in Fig. 1a; the mean density per trap varied from 1.44 to 33.73 (Fig. 1b). The large variation in the mean density by location might be owing to the geographic characteristics of the potato-cultivating areas. A large number of potato tuber moths was collected in potato fields adjacent to other crop fields, such as in Miryang and Seogwipo, whereas relatively low populations were observed in areas blocked by mountains and rivers. Therefore, it is deducible that potato tuber moths could migrate from other nearby crop-cultivating areas, enter the storage in the cultivation sites, and emerge in cultivated lands under favorable seasons (Hanafi, 1999; Rondon, 2010).

http://dam.zipot.com:8080/sites/kjoas/images/N0030470320_image/Figure_KJOAS_47_03_20_F1.png

Fig. 1. Locations of field survey (a) and mean density (b) of potato tuber moths in a trap. Values are presented as mean ± standard error of the mean (SEM).

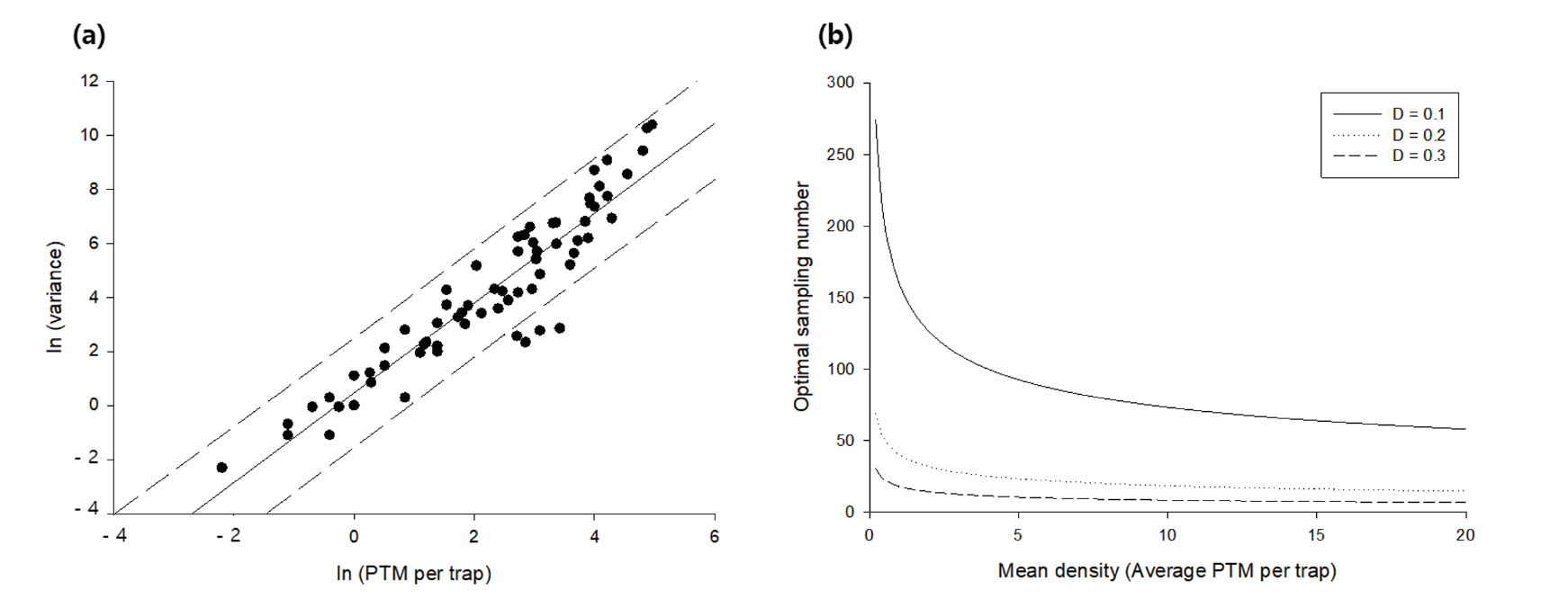
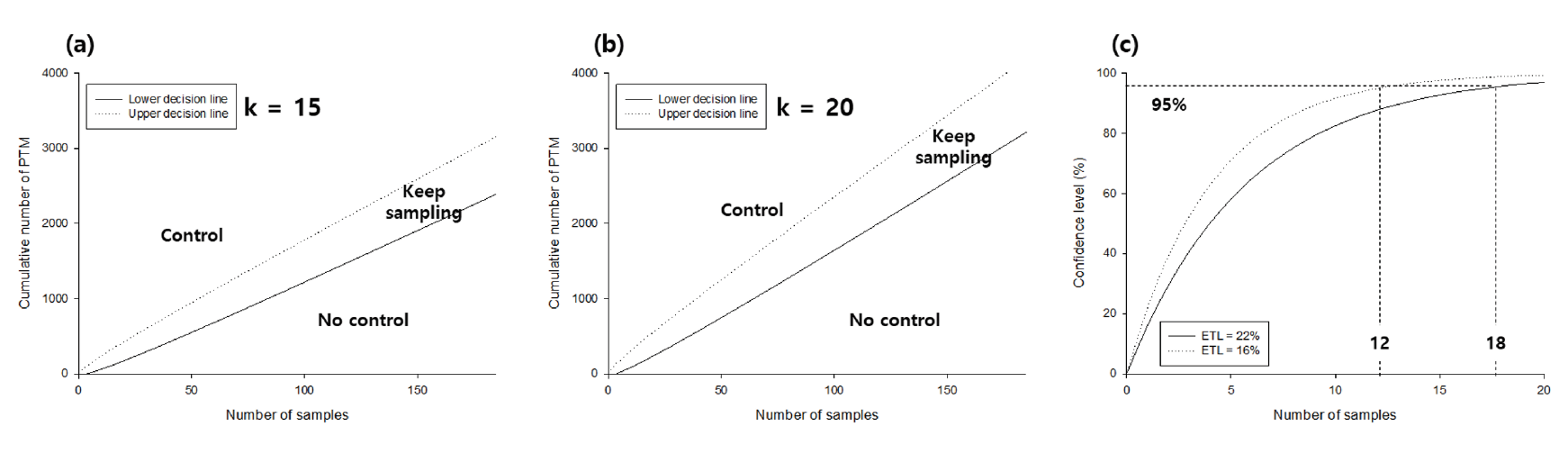
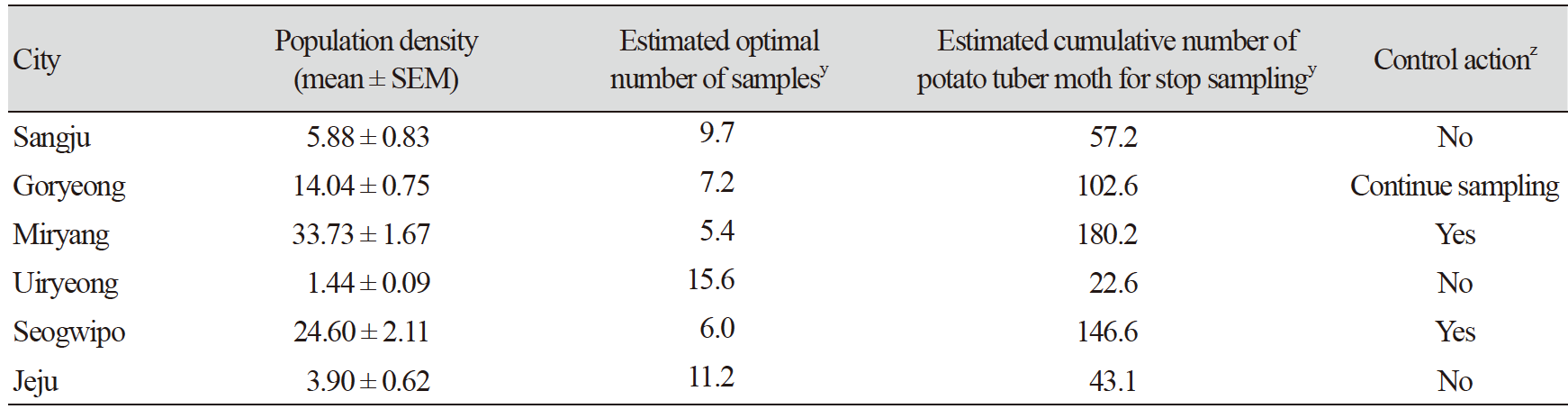
The TPL regression showed an R2 of 0.90, and the regression coefficient of b was 1.66 (p <0.05), suggesting that the distribution of potato tuber moth was aggregated (Fig. 2a) (Southwood, 1978; Hamilton and Hepworth, 2004). The optimal sampling number decreased with the increase in the mean density and decrease in the fixed precision level (Fig. 2b). This suggests that the precision level should be initially determined while designing field surveys, and the number of traps to be installed in the field should be determined by location. For example, Goryeong requires 65 and 7 traps at D = 0.1 and 0.3, respectively, but a higher number of traps is required at Sangju (88 and 10 traps at D = 0.1 and 0.3, respectively) because of the difference in the mean density between the two regions. From this perspective, in the future, field surveys should be conducted with increased number of traps to collect potato tuber moths. With respect to the location of installing traps, the edge of the field is adequate, as potato tuber moths tend to aggregate (Butler and Trumble, 2012). To establish the sequential stop line for sampling, the cumulative number of potato tuber moths was calculated using the number of sampled traps and the fixed precision level (Fig. 3). The number of samples to be collected decreased with the fixed precision level and the mean density, which is related to the cumulative number of potato tuber moths. For example, if 30 traps were installed in the field, the mean density should be larger than 130, 2.3, and 0.2 at D = 0.1, 0.2, and 0.3, respectively, to stop sampling. For practical application at D = 0.3 (Southwood, 1978), five traps might be necessary at Miryang, because the mean density was approximately 33.73 per trap, whereas the number of traps required at Uiryeong was 15 as the mean density was 1.44 per trap. The control decision was dependent on k (economic damage tolerance based on the mean density) and the number of potato tuber moths collected in traps (Fig. 4a and Fig. 4b). In Miryang, we collected 2,631 potato tuber moths from 78 traps during the entire field survey; thus, control actions might be needed as the upper control decision line at k = 15 and 20 was 1,418 and 1,875, respectively. In contrast, 141 potato tuber moths were collected from 24 traps; the lower control decision line at k = 15 and 20 was 222 and 304, respectively. Therefore, it is not necessary to take an action for controlling potato tuber moths in Sangju. In Goryeong, continuous sampling is still necessary because the cumulative number of potato tuber moths was 1,137 from 81 traps, located between the lower and upper control decision lines at k = 15. We estimated the optimal sampling numbers, cumulative number of potato tuber moth, and necessity of control action for each potato cultivation site using the developed sequential sampling method in this study (Table 1). In previous studies, the application of insecticides to chemically control the potato tuber moths was an important issue, while the effectiveness of biological control remains to be examined (Rondon, 2010). Recently, integrated pest management (IPM) has been used to control potato tuber moth (Abewoy, 2018), and the control action is determined using a cost–benefit analysis (Hagstrum and Flinn, 1996). Because the IPM programs include sampling to infer the pest population, sequential sampling is expected to be an effective approach in the program (Carvalho, 2016).

Because the standard of control decision was the economic threshold level, we calculated the number of samples required for deciding a control action using binomial sampling (Rondon, 2010; Abdallah, 2017). The minimum sample size was 12 and 18 to satisfy 95% confidence levels for detecting at least one potato tuber moth by sampling (Fig. 4c), depending on the economic threshold level proposed by Abewoy (2018). The difference between the sampling method by binomial distribution and sequential sampling method was that the former uses the fixed probability of potato tuber moth occurrence in the field (i.e., the economic threshold level in this study), whereas the latter dynamically changes the number of samples based on the observed number of potato tuber moths (Water, 1955). The sequential sampling method requires a larger number of samples than the binomial distribution method when the mean density is small with a high precision level, whereas fewer samples are needed when the mean density is large at a practical precision level (Cocco et al., 2015). Although binomial distribution might be useful and reduce the number of samples compared with that for sequential sampling at a low level of population (Butler and Trumble, 2012), it should be noted that the binomial distribution assumes a homogeneous mixture (Kim et al., 2019), that is, in this case, potato tuber moth is evenly distributed in the field. However, as shown in the aggregation index from the TPL analysis, the actual distribution was expected to be aggregated; thus, the sampling strategy using binomial distribution carries the risk of not accurately detecting the potato tuber moth in the field. Consequently, sequential sampling is adequate for sampling potato tuber moths in potato-cultivating fields. However, this study used the least number of traps; thus, to validate the developed sequential sampling method, further field surveys for potato tuber moth might be necessary with increased number of traps.

http://dam.zipot.com:8080/sites/kjoas/images/N0030470320_image/Figure_KJOAS_47_03_20_F2.png

Fig. 2. Regression analysis using the Taylor power law (TPL) to examine the spatial distribution of potato tuber moth in field (a), and plot to calculate the optimal sampling number by the mean density of potato tuber moth (PTM) (b).

http://dam.zipot.com:8080/sites/kjoas/images/N0030470320_image/Figure_KJOAS_47_03_20_F3.png

Fig. 3. Sequential stop lines for evaluating potato tuber moth (PTM) population in potato cultivation areas by D = 0.1 (a), D = 0.2 (b), and D = 0.3 (c). Ntoe the different Y-axis scales.

http://dam.zipot.com:8080/sites/kjoas/images/N0030470320_image/Figure_KJOAS_47_03_20_F4.png

Fig. 4. SControl decision line for potato tuber moth (PTM) at k = 15 (a), and k = 20 (b) and estimated number of samples to meet 95% confidence level to detect potato tuber moth at a fixed economic threshold level (ESL) using binomial distribution (c). ETL, economic threshold level.

Table 1. Estimated sample number, stop line, and control action for potato tuber moth monitoring in areas of potato cultivation.

http://dam.zipot.com:8080/sites/kjoas/images/N0030470320_image/Table_KJOAS_47_03_20_T1.png

SEM, standard error of the mean.

^y Both values were estimated at the desired precision level of D = 0.3.

^z Control action was set at k = 15, which is the value of economic damage tolerance at the density of pests requiring control.

Conclusion

In this study, we developed a sequential sampling method for collecting potato tuber moths in potato cultivation fields based on empirical and statistical approaches. As sequential sampling depends on the mean density of potato tuber moth, the number of samples should be determined by the population of potato tuber moths at the appropriate precision level. Consequently, we propose that a larger sample size is necessary in fields with a low number of potato tuber moths and vice versa in fields where potato tuber moths are actively observed. In addition, this sampling approach provides a quick method to determine the control action based on the cumulative number of potato tuber moths collected using sample traps. Finally, when installing traps in a field to monitor potato tuber moths, the surrounding terrain should be considered because our field survey showed that the density of potato tuber moths changed according to the surrounding environment.

Conflict of interest

The authors declare that there is no conflict of interest.

Acknowledgements

This work was carried out with the support of “Cooperative Research Program for Agricultural Science & technology Development (Project No. PJ0134642018)”, Rural Development Administration, Republic of Korea.

Authors Information

Jae-Min Jung, https://orcid.org/0000-0003-3975-542X

Dae-hyeon Byeon, https://orcid.org/0000-0003-4619-2186

Eunji Kim, https://orcid.org/0000-0001-7986-8141

Hye-Min Byun, https://orcid.org/0000-0001-7218-8899

Jaekook Park, https://orcid.org/0000-0001-6965-7199

Jihoon Kim, https://orcid.org/0000-0001-5605-9325

Jongmin Bae, https://orcid.org/0000-0002-4292-3634

Kyutae Kim, https://orcid.org/0000-0003-4061-6427

Marcos Roca-Cusachs, https://orcid.org/0000-0002-9174-6021

Minjoon Kang, https://orcid.org/0000-0002-6522-6102

Subin Choi, https://orcid.org/0000-0001-8544-0168

Sumin Oh, https://orcid.org/0000-0003-2674-0069

Sunghoon Jung, https://orcid.org/0000-0001-6086-0326

Wang-Hee Lee, https://orcid.org/0000-0002-8834-1779

References

1 Abdallah YE. 2017. Yield losses caused to potato plants by potato tuber worm, Phthorimaea operculella (Zeller) and its economic levels at Qalyubyia Governorate. Egyptian Academic Journal of Biological Sciences. A, Entomology 10:73-79.

2 Abewoy D. 2018. Review on potato late blight and potato tuber moth and their integrated pest management options in Ethiopia. Advances in Crop Science and Technology 6:331.

3 Butler CD, Trumble JT. 2012. Spatial dispersion and binomial sequential sampling for the potato psyllid (Hemiptera: Triozidae) on potato. Pest management science 68:865-869.

4 Carvalho MO. 2016. Developing and validating sequential sampling plans for integrated pest management on stored products. Advanced Techniques in Biology and Medicine 4:2379-1764.1000183.

5 Choe H, Kang J, Jung H, Choi S, Park JJ. 2017. Development of sequential sampling plans for Tetranychus urticae in strawberry greenhouses. Korean Journal of Environmental Biology 35:427-436. [in Korean]

6 Choi W, Park JJ. 2015. Development of sequential sampling plan for Bemisia tabaci in paprika greenhouses. Korean Journal of Applied Entomology 54:159-167. [in Korean]

7 Cocco A, Serra G, Lentini A, Deliperi S, Delrio G. 2015. Spatial distribution and sequential sampling plans for Tuta absoluta (Lepidoptera: Gelechiidae) in greenhouse tomato crops. Pest management science 71:1311-1323.

8 Giles KL, Royer TA, Elliott NC, Kindler SD. 2000. Development and validation of a binomial sequential sampling plan for the greenbug (Homoptera: Aphididae) infesting winter wheat in the southern plains. Journal of Economic Entomology 93:1522-1530.

9 Green RH. 1970. On fixed precision level sequential sampling. Population Ecology 12:249-251.

10 Hagstrum DW, Flinn PW. 1996. Integrated pest management. In Integrated Management of Insects in Stored Products edited by Subramanyam BH, Hagstrum DW. pp. 399-408. Marcel Dekker, New York, USA.

11 Hamilton AJ, Hepworth G. 2004. Accounting for cluster sampling in constructing enumerative sequential sampling plans. Journal of Economic Entomology 97:1132-1136.

12 Hamilton AJ, Schellhorn NA, Endersby NM, Ridland PM, Ward SA. 2004. A dynamic binomial sequential sampling plan for Plutella xylostella (Lepidoptera: Plutellidae) on broccoli and cauliflower in Australia. Journal of Economic Entomology 97:127-135.

13 Hanafi A. 1999. Integrated pest management of potato tuber moth in field and storage. Potato Research 42:373-380.

14 Iwao SI. 1975. A new method of sequential sampling to classify populations relative to a critical density. Researches on Population Ecology 16:281-288.

15 Jung JM, Lee SG, Kim KH, Jeon SW, Jung S, Lee WH. 2020. The potential distribution of the potato tuber moth (Phthorimaea operculella) based on climate and host availability of potato. Agronomy 10:12.

16 Karandinos MG. 1976. Optimum sample size and comments on some published formulae. Bulletin of the ESA 22:417-421.

17 Kim DG, Cho BK, Lee WH. 2016. A novel approach in analyzing agriculture and food systems: Review of modeling and its applications. Korean Journal of Agricultural Science 43:163-175.

18 Kim DG, Lee SH, Cho BK, Byeon DH, Lee J, Lee WH. 2019. Statistical and empirical determination of the optimal sampling method for detecting non-homogeneously mixed living modified organisms (LMO) seeds. Journal of Crop Science and Biotechnology 22:299-307.

19 Kim DG, Lee SH, Cho BK, Byeon DH, Lee J, Lee WH. 2020. Statistical analysis for determining optimal sample size for living modified organism (LMO) seed detection. Journal of Crop Science and Biotechnology 23:1-7.

20 Kroschel J, Sporleder M, Tonnang HEZ, Juarez H, Carhuapoma P, Gonzales JC, Simon R. 2013. Predicting climate-change-caused changes in global temperature on potato tuber moth Phthorimaea operculella (Zeller) distribution and abundance using phenology modeling and GIS mapping. Agricultural and Forest Meteorology 170:228-241.

21 Kwon M, Kim J, Maharjan R, Choi JY, Kim GH. 2017. Change in the distribution of the potato tuber moth, Phthorimaea operculella (Zeller)(Lepidoptera: Gelechiidae), in Korea. Journal of Asia-Pacific Entomology 20:1249-1253.

22 Maharjan R, Jung C. 2011. Rearing methods of potato tuber moth, Phthorimaea operculella (Zeller) (Lepidoptera: Gelechiidae). Korean Journal of Soil Zoology 15:53-57

23 Manly BF. 1989. A review of methods for the analysis of stage-frequency data. In Estimation and analysis of insect populations edited by Manly B, McDowell L. pp. 3-69. Springer, New York, USA.

24 Nam YW, Chun YS, Ryoo MI. 2009. Developing sequential sampling plans for evaluating maize weevil and Indian meal moth density in rice warehouse. Korean Journal of Applied Entomology 48:45-51.

25 Raman KV, Palacios M. 1982. Screening potato for resistance to potato tuberworm. Journal of Economic Entomology 75:47-49./

26 Rondon SI. 2010. The potato tuberworm: A literature review of its biology, ecology, and control. American Journal of Potato Research 87:149-166.

27 Saxena AP, Rizvi SMA. 1974. Insect pest problems of potatoes in India. Journal of the Indian Potato Association 1:45-50.

28 Serra GV, Porta NCL, Avalos S, Mazzuferi V. 2013. Fixed-precision sequential sampling plans for estimating al-falfa caterpillar, Colias lesbia, egg density in alfalfa, Medicago sativa, fields in Córdoba, Argentina. Journal of Insect Science 13:41.

29 Song JH, Yang CJ, Shim HS, Jwa CS. 2015. Development of sequential sampling plan for bacterial leaf blight of garlic by cluster sampling. Research in Plant Disease 21:268-272.

30 Southwood TRE. 1978. Ecological methods with particular reference to the study of insect populations. p. 524. John Wiley and Sons, New York, USA.

31 Taylor LR. 1961. Aggregation, variance and the mean. Nature 189:732-735.

32 Taylor LR. 1965. A natural law for the spatial disposition of insects. pp. 396-397. In proceedings of the 12th International Congress on Entomology, London, UK.

33 Water WE. 1955. Sequential sampling in forest insect surveys. Forest Science 1:68-79.

34 Wise IL, Lamb RJ. 1995. Spatial distribution and sequential sampling methods for the potato aphid, Macrosiphum euphorbiae (Thomas) (Homoptera: Aphididae), in oilseed flax. The Canadian Entomologist 127:967-976.