Introduction
축산물 이력제도는 축산농가의 생산, 이동, 출하에 대한 모든 거래내역을 기록 및 관리함으로써 축산농가에 대한 방역의 효율성을 도모하고, 축산물 유통에 대한 투명성을 높여, 원산지 허위표시 등 둔갑 판매 방지로 축산업 및 관련산업의 건전한 발전에 이바지하기 위해 필요한 제도이다. 본 연구에서 활용된 돼지 이력제도는 2012년 10월 돼지고기 이력제도 시범사업 추진 후 2014년 12월 전면 시행되었다(KAPE, 2020).
한돈 이력제는 사육, 도축, 가공, 판매 단계로 관리된다. 사육단계에서 축산농가는 발급받은 6자리 농장식별번호를 모든 돼지에 표시하게 되며, 매월 사육현황을 이력시스템에 신고하고, 이동 시 이동 내역을 신고해야한다. 특히, 비육돈과 달리 종돈은 개체단위 식별을 위한 12자리 이력번호를 표시한다.
도축단계에서는 출하농장별로 분리 수송하여 운송 시 농장 간에 돼지가 섞이지 않도록 하며, 도축 전 농장식별번호를 표시하고, 이력시스템 등록여부 및 신고내용과 실제 출하두수를 확인한다. 또한, 도축 후 반출되기 전에 12자리 이력번호를 지육에 표시한다. 가공단계에서는 지육 매입 시, 이력번호와 거래내역서의 일치를 확인하고, 이력시스템에 입력한다. 가공 및 포장 처리는 이력변호별로 실시하는게 원칙이나, 이력번호 단위별로 가공이 어려울 수 있어 15자리 묶음번호를 사용할 수 있다. 가공 이후에는 개별 포장지 겉면에 이력번호 및 묶음번호를 표시하여 반출 및 판매한다. 판매단계/판매장에서는 모든 거래내역서를 기록, 신고해야 한다.
이러한 축산물이력정보는 질병발생 시 농장단위별로 추척 및 관리할 수 있다는 장점 이외에 수급관리측면에서 정보의 활용도가 높다. 그러나 현재까지 이력정보를 이용한 월별 수급예측모형 개발 및 정보 활용도 측면에서 이력정보의 평가에 관한 연구는 제한적이다.
본 연구의 목적은 축산물품질평가원(KAPE, 2020)의 월별 시계열자료인 한돈 이력정보데이터를 이용하여, 돼지의 출생과 성장, 도축/출하 등 생물학적 특성을 반영한 코호트(cohort) 기법과 동태적 생태방정식 모형(dynamic ecological equation model, DEEM) 체계를 구축하여 미래 출하 가능 마릿수 및 공급량을 예측하고, 경제이론에 부합된 정책 시뮬레이션이 가능한 월별 한돈모형을 구축하는데 있다. 또한 구축된 모형을 기반으로 한돈 이력정보 활용성에 대한 평가와 시사점을 도출하고자 한다. 따라서 본 연구를 통해 생산자의 의사결정과 정부의 수급 관련 정책 방향을 설정하는 기초자료로 활용하는데 목적이 있다.
Materials and Methods
이력제 모돈
본 연구에서 사용한 KAPE (2020)의 한돈 이력제 자료는 돼지고기 이력제 시범사업 추진 후 2014년 12월부터 2020년 8월까지 월별 자료이다. 돼지 이력제 자료는 원종돈(great grand parent, GGP), 종돈(grand parent, GP), 모돈(parent stock, PS), 후보돈, 웅돈 마릿수를 제공하며, 비육돈 마릿수는 월령에 따라 자돈(0 - 2개월), 육성돈(2 - 4개월), 비육돈(4 - 6개월)로 구분된다.
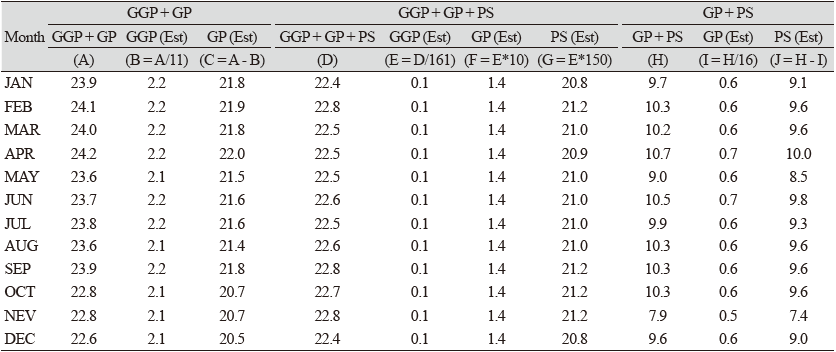
Table 1에서 볼 수 있듯이, 모돈 이력제 데이터 자료는 KAPE (2020) 자료를 이용하였다. 돼지 이력제는 모돈(PS)으로 부터 시작된다. 다만, 신고된 사업의 형태가 원종돈(GGP), 종돈(GP), 모돈(PS), 인공수정(artificial insemination, AI)을 혼용하여 생산하는 모돈 사육농장이 전체 모돈 마릿수에서 약 6%에 해당한다. GGP, GP, PS, AI를 구별하여 생산, 신고하는 마릿수는 전체 모돈 수의 약 94%에 해당한다. 이력제 시행 이후, 2020년까지 사업형태별로 구분하여 생산, 신고하는 농장의 전체 모돈 마릿수는 94.1 - 94.5% 범위로 나타났다.
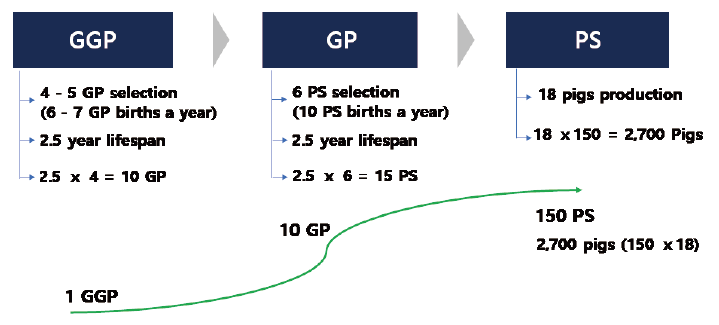
따라서 이력제자료의 모돈(PS)마릿수는 보완 및 추정이 필요하다. GGP, GP, PS, AI를 혼용하여 생산하는 농장의 모돈 마릿수를 사업형태별로 분리하기 위해서는 몇가지 가정이 필요하다. 즉 Fig. 1에서 볼 수 있듯이, GGP, GP, PS 관계의 코호트 별 생산 마릿수를 가정한다. GGP에서 GP, 그리고 PS로 생산하고 선발되는 마릿수 비율을 적용하면, Table 1과 같이 사업형태별 모돈 마릿수를 추정 및 계산할 수 있다.
이력제 모돈 데이터에 따르면, 사육 마릿수는 2019년까지 증가추세이나, 2020년 이후 감소세를 보이고 있다. 원종돈(GGP) 사육 마릿수는 약 1만 마리 내외 수준이며, 종돈(GP)은 5만 5천 마리 수준이다. 모돈(PS)은 약 90만 마리 수준으로 나타나, 전체 모돈 사육 마릿수는 약 100만 마리 내외 수준이다.
이력제 비육돈
모돈에서 생산된 비육돈은 이유 이후, 체중이 약 20 - 25 kg 정도인 60 - 70일령부터 비육한다. 이력제의 비육돈은 월령에 따라 2개월 간격으로 0 - 2개월령은 자돈, 3 - 4개월령은 육성돈, 5 - 6개월령은 비육돈으로 구분된다. Table 2에서 볼 수 있듯이, 동물의 생장 기간을 고려한 코호트 분석을 통해, 모돈(PS)의 임신 기간을 고려하여 4 - 5개월전의 모돈 마릿수 대비 당월 0 - 2개월의 자돈 마릿수 비율은 평균 약 4.2마리로 계산된다. 1 - 2개월 전 0 - 2개월의 자돈(F1) 대비 당월 3 - 4개월 육성돈(F2) 마릿수 비율은 평균 0.88마리로 계산되며, 1 - 2개월 전의 3 - 4개월 육성돈(F2) 대비 당월 5 - 6개월 비육돈(F3) 마릿수 비율은 평균 1.04마리로 계산되었다. 여기서 육성돈(3 - 4개월)/자돈(0 - 2개월)의 비율은 평균 0.88마리로 0.12마리는 폐사율로 추정할 수 있다. 이는 자돈에서 폐사율이 높은 한돈 특성을 반영하는 것으로 판단된다. 다만, 비육돈(5 - 6개월)/육성돈(3 - 4개월) 비율은 폐사율을 감안한다고 하더라도 1.0보다 높게 나타나, 5 - 6개월 비육돈 이력제 데이터에는 6개월 이상의 비육돈 마릿수도 포함된 것으로 추정된다. 따라서 비육돈 추정은 코호트 분석으로는 한계가 존재한다.
이력제 비육돈 데이터에 따르면, 사육 마릿수는 과거 증가추세를 보이다가, 2020년 이후 감소세를 보이고 있다. 0 - 2개월 자돈 마릿수는 2020년 8월 386만 5천 마리 수준이며, 3 - 4개월 육성돈 마릿수는 341만 3천 마리, 5 - 6개월 비육돈은 350만 3천마리 수준으로, 전체 비육돈(자돈 + 육성돈 + 비육돈) 마릿수는 1,078만 마리 수준을 보이고 있다.
Table 2. The number of pigs by month in animal products traceability. Unit: Head 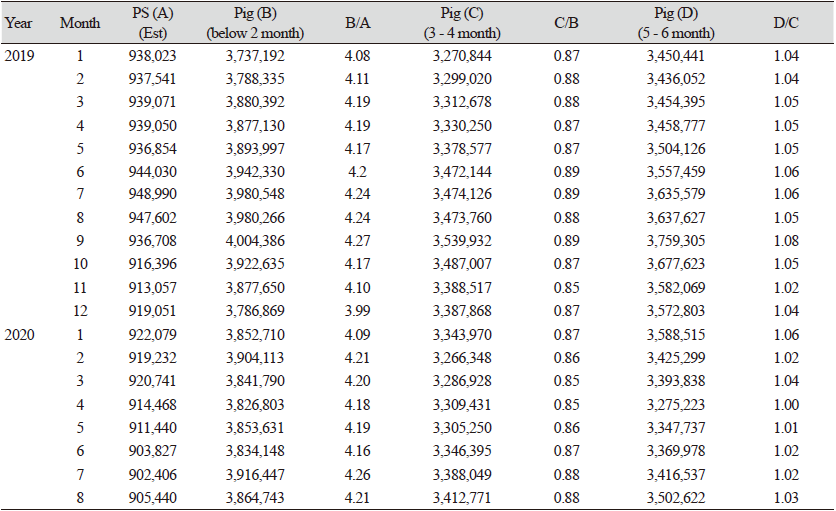
|
|
PS, parent stock. Source: KAPE, 2020. |
도축마릿수 및 생산량
모돈에서 생산된 비육돈은 자돈, 육성돈, 비육돈으로 성장하면서 약 6개월령인 160일 이상이 되면, 시장에 출하하게 되는 110 kg 정도의 체중에 이르게 된다.
도축 또는 출하 마릿수 예측을 위해서 코호트 분석을 적용하면, Table 3에서 볼 수 있듯이, 도축 마릿수/비육돈(5 - 6개월)의 비율은 평균 약 0.42마리로 계산된다. 도축 마릿수가 계산되면, 축산물품질평가원(KAPE, 2020)의 정육환산비율을 적용하여 정육 생산량으로 환산하는데, 추정식은 아래와 같다. 도축 마릿수에 77%를 곱하면 지육 생산량이 계산되고, 여기에 다시 65.7%를 곱하면 정육생산량이 된다.
Table 3. The number of slaughter in animal products traceability. Unit: Head,ton 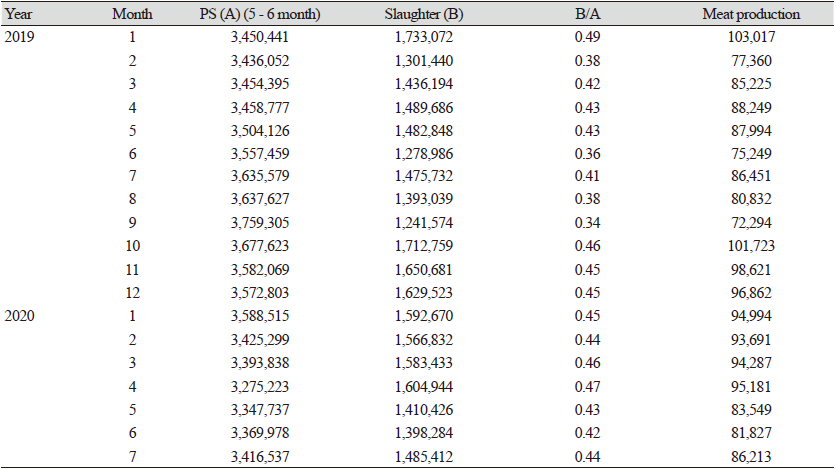
|
|
Source: KAPE, 2020. |
$Q_{carcass_{t}} = SL × SLW × 0.77 $ (1)
$Q_{meat_{t}} = Q_{carcass_{t}} × 0.657$ (2)
$SL$ : 도축마릿수, $SLW$ : 도체중, $Q_{carcass_{t}}$: 지육생산량, $Q_{meat_{t}}$: 정육생산량
이력제 모돈 데이터에 따르면, 도축마릿수 추세는 모돈(PS)과 비육돈 추세와 비슷하여 2020년이후 감소세를 보이고 있으며, 2020년 7월 148만 5천마리 수준이며, 이를 환산한 정육생산량은 8만 6천톤 수준이다.
Results and Discussion
모형 구조
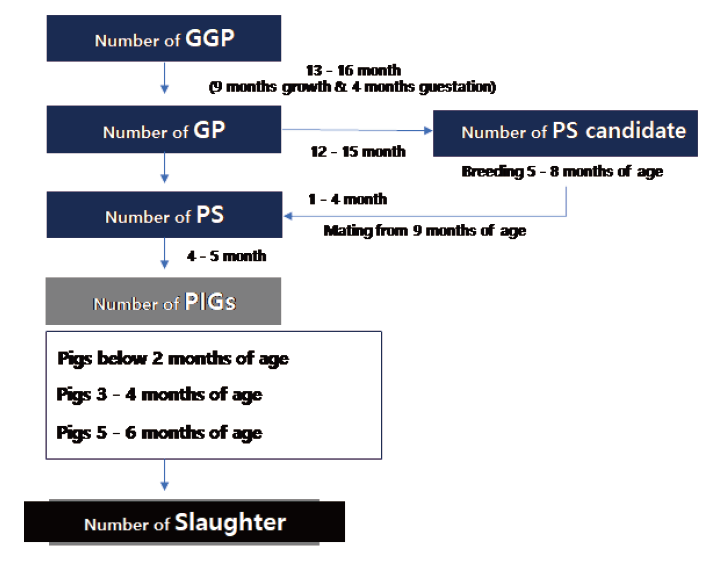
본 연구는 축평원의 월별 시계열자료인 이력정보데이터를 이용하고, 필요데이터는 보완 및 생성하여, 돼지의 출생과 성장, 도축/출하 등 생물학적 특성 및 생육기간을 반영한 코호트(cohort)기법과 Han 등(2016; 2021)연구에서와 같이 동태적 생태방정식 모형(DEEM) 체계를 구축하였다. 따라서 Fig. 2와 같이 생태학적 모형 구축을 위한 돼지 생장 단계 및 모형 구조를 설계하였다. 번식돈의 경우 출생 후, 25 - 30일(체중이 6 - 8 kg) 이후 이유를 하게 되며, 이후 육성 기간을 거쳐 약 8 - 10개월(평균 9개월)이 되면 체중 120 - 140 kg에 달하게 되고, 웅돈를 통해 임신하게 된다. 또한 약 114일(4개월)간의 임신 기간 이후 분만을 하게 된다. 돼지의 원종돈(GGP)는 평균 9개월의 생장과 임신 4개월을 거쳐 종돈(GP)을 생산한다. 종돈(GP)은 약 6 - 7마리 생산하고, 이중 4 - 5마리가 선발된다. 후보돈(PS candidate)은 번식돈에 편입된 5 - 8개월의 암퇘지를 말하는 것으로, 모돈(PS)이전의 암퇘지이다. 농가에서는 약 90 kg정도의 5 - 8개월령의 후보돈을 입식하여 1 - 4개월 정도 사육 후 9개월령부터 모돈(PS)으로 활용한다. 즉, 현재의 후보돈(PS candidate) 마릿수는 종돈(GP)의 임신기간 4개월과 5 - 8개월령의 후보돈(PS candidate) 생장 기간을 더하면 12 - 15개월 전의 종돈(GP)마릿수에 의해 결정된다. 따라서 GGP에서 생산되어 선발된 GP, 그리고 GP에서 생산되어 선발된 후보돈(PS_candidate), 그리고 PS의 생장(약 9개월), 임신(약 4개월), 비육돈의 생육기간(약 6개월), 출하시기를 시차를 고려한 생육함수를 도출하고, 월별 도축마릿수 및 출하량을 예측하도록 모형화 하였다. 또한, 식(3) - 식(6)과 같이, 각 방정식에는 경제이론에 부합된 소득의 대리 변수인 도매가격/사료가격을 설명변수에 포함하였다. 다만, 공급량 추정의 한계점으로 연도별/계절별 상이한 폐사율이 데이터가 존재하지않아, 직접 적용하지 않고 각 생육단계별 방정식에 회귀하였다.
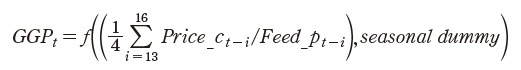 (3)
(3)
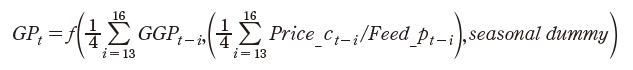 (4)
(4)
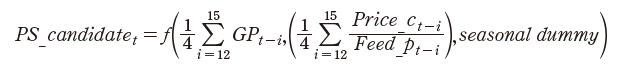 (5)
(5)
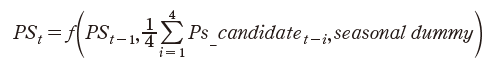 (6)
(6)
PS : 모돈, PScandidate : 후보돈, Price_c : 지육도매가격, Feed_p : 사료가격
종돈(GP)에서 후보돈(PS_candidate)이 생산/선발되어 일정기간 성장 후, 모돈(PS)으로 성장하면, 임신 4개월의 시차를 고려하여 모돈(PS)에서 생산되는 자돈(0 - 2개월)이 예측된다. 이후 월령에 따라 3 - 4개월의 육성돈, 5 - 6개월의 비육돈은 코호트 분석으로 예측할 수 있으나, 월령별/계절별 폐사율을 적용하지 못하여, 모형설계에서는 계절 더미만 고려하고, 식(7) - 식(9)와 같이 회귀분석하였다. 다만, 비육돈(5 - 6개월)/육성돈(3 - 4개월) 비율은 폐사율을 감안한다고 하더라도 1.0보다 높게 나타나, 5 - 6개월 비육돈 이력제 데이터에는 6개월 이상의 비육돈 마릿수도 포함된 것으로 추정된다. 따라서 식(9)에서처럼, 추정될 금기(t)의 비육돈(F3)의 모형방정식은 전기(t-1)의 비육돈(F3)과 육성돈(F2)에서 금기(t)의 도축 마릿수를 제외하도록 설계하였다.
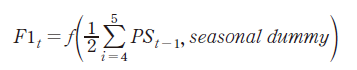 (7)
(7)
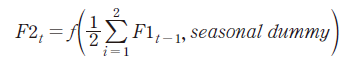 (8)
(8)
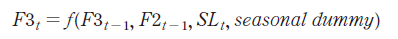 (9)
(9)
F1: 자돈, F2 : 육성돈, F3: 비육돈, SL: 도축마릿수
5 - 6개월 비육돈(F3)의 체중이 110 kg이상이 되면, 시장에 출하되게 된다. 도축 마릿수 또는 출하 마릿수의 예측은 식(10)과 같이, 전월의 비육돈(F3)의 함수로 구성하며, 설명변수에 계절 더미를 추가하였다. 또한, 예측된 도축마릿수에 도축체중을 곱하면 생체기준의 도축물량이 계산된다.
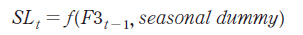 (10)
(10)
F3: 비육돈, SL: 도축마릿수
도축 물량(생체기준)이 계산되면 식(1)과 식(2)와 같이 지육 생산량을 계산하며, 지육 생산량에서 다시 정육 생산량으로 환산한다. 정육 생산량이 계산되면, Table 4와 같이 부위별 정육율을 이용하여 부위별 생산량이 계산된다.
모형 추정결과
본 연구에서는 돼지고기 이력제 시범사업 추진 후 2014년 12월부터 2020년 8월까지의 이력제 데이터를 이용하여, 생장 및 임신을 고려하고, 계절성을 고려한 생육단계별 사육 마릿수를 추정하였으며, 월별 데이터로 자기 상관 문제가 자주 발생하여 GLS방법을 선택하지 않고 자기상관 구간에 더미 변수를 사용하여 문제를 해결하였다. 즉, Han 등(2021)에서 사용한 방법으로, 잔차(residual)가 0을 기준으로 양(+) 또는 음(-)으로 일정 기간 지속하였다가 부호가 변하는 시점에 구조 더미 변수(SD) 또는 더미 변수를 추가하는 방법을 사용하였다. Wooldridge (2005)에 따르면, 일반적으로 자기 상관 문제를 해결하기 위한 GLS방법으로 AR, MA 변수를 사용하나, 자기상관이 심할 경우나, 자기상관에 대한 모형 설정을 잘못할 경우에는 GLS방법을 사용하더라도, 추정된 파라미터 값에 편의(bias)가 발생하기 때문이다(Han et al., 2021).
또한, 자기상관문제로 표준편차(standard error)를 계산할 공분산(covariance)은 전통적인 공분산(covariance)을 사용하지 않고, Newey-west HAC (Heteroskedasticity & Autocorrelation Covariance)를 사용하였다.
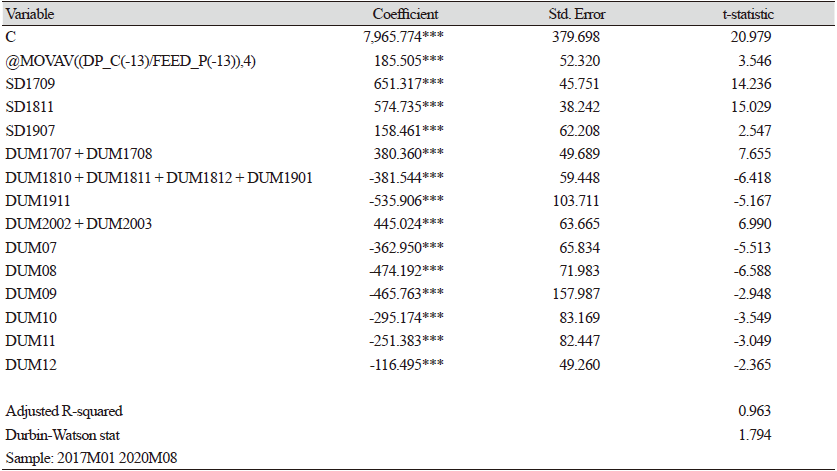
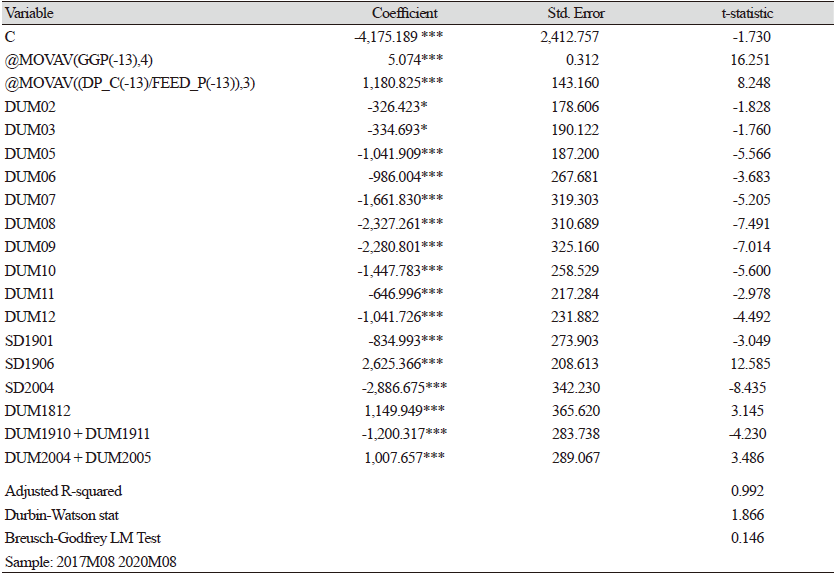
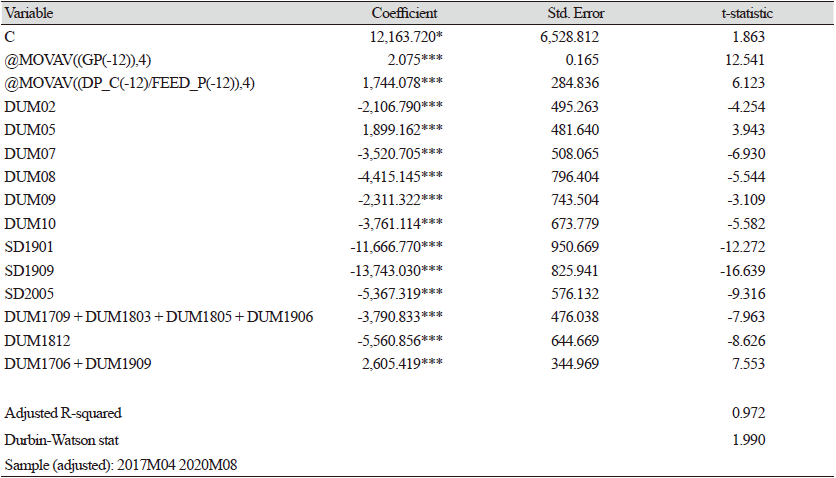
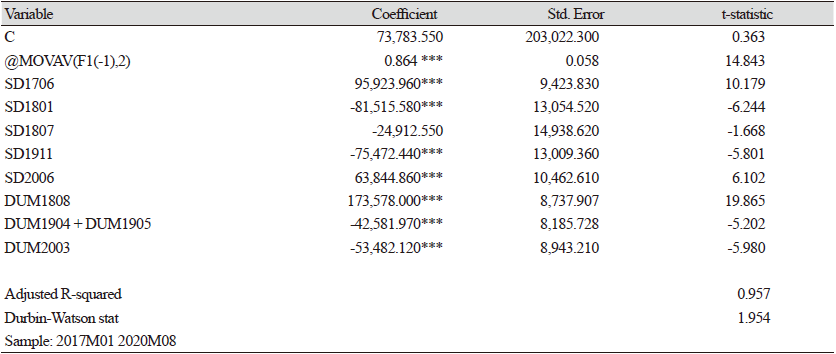
각 단일방정식별 추정결과, Table 4에서와 같이, 돼지 원종돈(GGP)의 생장 및 임신기간을 고려하여 모형화 하였고, 소득변수(도매가격/사료가격)와 계절 더미를 고려하여 단일방정식을 구성하였다. 돼지의 생육 및 임신 기간을 고려한 13∼16개월 전의 평균 소득에 대한 계수는 185.5로 계측되었다. 이는 13 - 16개월 전의 평균소득 1단위가 늘어나면, 원종돈(GGP)이 185.5마리 늘어난다는 의미이다. 해석을 쉽게 하고자 탄력성으로 환산하여 해석하면 0.14로 추정된다. Table 5에서, 9개월의 성장 기간과 4개월의 임신 기간을 고려한 13 - 16개월 전의 원종돈(GGP) 1마리가 증가하면, 종돈(GP)는 5.07마리 증가하는 것으로 추정되어, Fig. 1에서와 같이 GGP에서 생산된 GP가 1년에 4 - 5마리 선발되는 것과 부합된다. Cagan (1956)의 적응적 기대가설모형(adaptive expectation model)으로, 전기의 사료가격대비 가격(Price_ct − i/Feed_pt − i)을 소득의 대리변수로 사용하였다. GP 사육 마릿수에 대한 소득의 탄력성은 0.17로 추정되었으며, 월별 계절더미를 반영하였다.
또한, SD1901, SD1906, SD2004의 구조 더미 변수 및 더미 변수를 사용하여 자기 상관 문제를 완화하였다. 그리고, 특성이 유사한 더미 변수는 서로 더하여 자유도를 높였다.
Table 6에서, 12 - 15개월 전의 종돈(GP)이 1마리 증가하면, 후보돈(PS_candidate)은 2.08마리 증가하는 것으로 추정되었다. 종돈(GP)은 자돈을 1년간 약 10마리를 생산하고, 6마리를 후보돈으로 선발한다. 후보돈은 5 - 8개월령의 약 4개월간의 누적 마릿수라는 점을 고려할 때 계수 2.08로 추정된 것은 6마리(2마리*3 = 6)와 일치한다. 동기간의 사육 마릿수에 대한 소득의 탄력성은 0.12로 추정되었다.
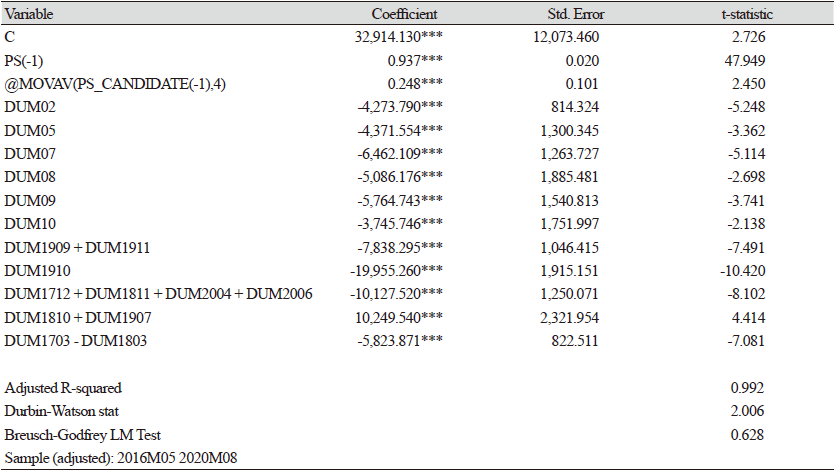
Table 7에서, 전기 모돈($PS_{t−1}$)의 계수는 0.94로 추정되었는데, Nerlove (1956)의 PAM(부분조정)모형으로 해석할 수 있다. 식(11)과 같이, 동태적 접근방식 중 하나인 Nerlove의 부분조정모형은 희망공급량(desired supply)에 접근하는 실제 공급량(actual supply)의 속도(speed)와 수준(level)을 분석한다. 특히, 조정계수(δ)는 하나의 제약조건이 존재하는데 반드시 0보다 크고 1보다 작아야 한다. 만약에 조정계수가 1보다 크다면 무작위 행보(random walk)현상이 발생한다. 즉, 비안정적(non-stationary)현상이 되며, 동태적(dynamically)으로 수렴(convergent)하지 않게 된다. 조정계수가 1에 근접할수록 희망공급량(desired supply)에 대한 실제 공급량의 조정속도가 빨라지게 된다. 반면 조정계수가 0에 근접할수록 조정속도는 느려진다.
식(11), 널러브의 부분조정모형(Nerlovian partial adjustment model)를 이용하여 동태적 공급반응함수가 구성되며 $q_{t}$*결과에 대해 함수형태가 결정된다. 부문조정모형은 희망투자와 실제 투자의 속도를 나타내는 모형이다. 즉, 식(11)을 식(12)에 대입하면 식(13)의 동태적 공급반응함수형태가 생성된다.
$(q_{t} − q_{t − 1}) = \delta(q_{t}* − q_{t − 1}) subject to 0 < \delta < 1$ (11)
$q_{t}* = β_{0} + β_{1pt}* + β_{2zt} + e_{t}$ (12)
$q_{t} = \deltaβ_{0} + \deltaβ_{1pt}* + \deltaβ_{2zt} + \delta e_{t} + (1 − \delta)q_{t − 1}$ (13)
$q_{t}$: actual supply, $q_{t}$*: desired supply, $\delta$: adjustment coefficient, $p_{t}$*: expected price, $z_{t}$: other fators, et: error term
여기서 전기 모돈($PS_{t−1}$)의 추정된 속도조정계수(σ)가 0.06 (= 1 - 0.94)으로 조정속도가 매우 느리다는 것으로, 전월의 모돈(PS) 사육 마릿수와 당월의 모돈(PS) 사육 마릿수 차이가 크게 없다는 것을 의미한다.
1 - 4개월 전의 후보돈(PS_candidate) 마릿수가 1마리 증가하면, 모돈(PS)은 0.25마리 증가하는 것으로 추정되었는데, 누적 4개월(5 - 8개월령)의 후보돈 마릿수 합계로 전월 후보돈 중에서 당월 모돈(PS)으로 선발되는 마릿수를 뜻한다. 즉, 계수 0.25마리 의미는 평균적으로 $\frac {1} {4}$마리가 되므로 생육행태와 일치하는 것으로 판단된다.
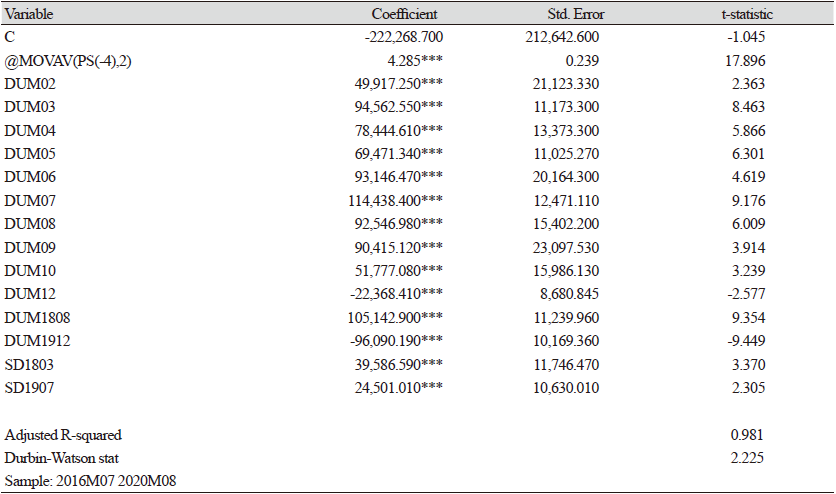
Table 8에서, 임신기간을 고려한 4 - 5개월 전의 모돈(PS) 마릿수가 1마리 증가하면, 2개월 미만의 자돈(F1)은 4.18마리 증가하는 것으로 추정되었다. 특히, 설명변수 중 4 - 5개월 전의 평균 모돈(PS)을 사용한 이유는 2개월 미만의 자돈(FI)의 육성 단계별 기간이 2개월로 구분되기 때문이다. 또한, 모돈(PS)의 PSY (연간 모돈 두당 이유두수)가 약 23마리 내외라는 점을 감안하면 생육행태와 일치하는 것으로 판단된다.
Table 9에서, 0 - 2개월령 자돈(F1)이 예측되면, 이후 코호트(cohort)로 월령에 따라 3 - 4개월령 육성돈(F2)이 예측된다. 1 - 2개월 전 0 - 2개월령 자돈 (F1)마릿수가 1마리 증가하면, 육성돈(F2)은 0.86마리 증가하는 것으로 추정되었다.
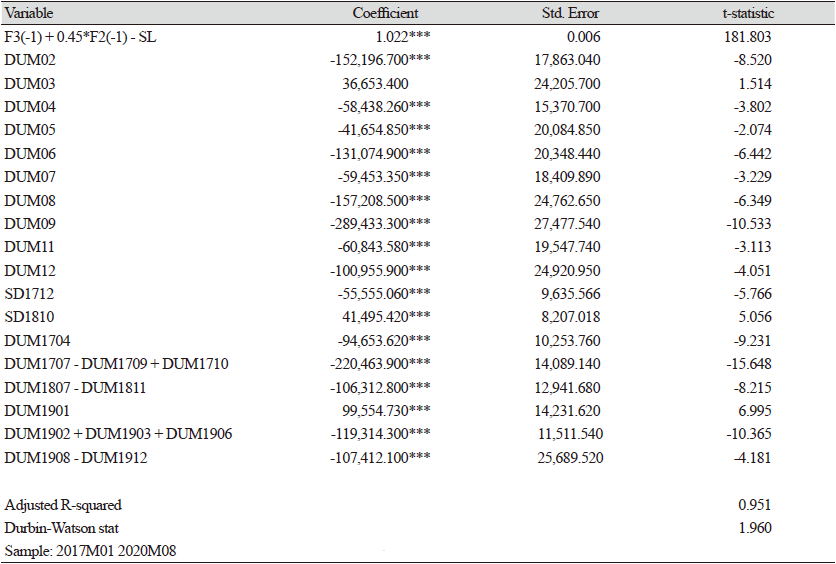
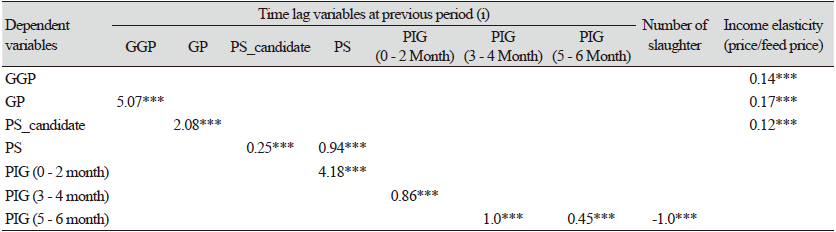
Table 10에서, 비육돈(F3) 마릿수 추정은 식(9)에서 설명한 것처럼, 1 - 2개월 전의 육성돈(F2)대비 비육돈(F3) 마릿수의 비율이 1.0보다 크게 나타나, 비육돈(F3)은 5 - 6개월의 비육돈 뿐만 아니라, 6개월 이상의 비육돈 마릿수도 포함된 것으로 판단하였다. 따라서, 금기(t)의 비육돈(F3)의 모형방정식은 전기(t-1)의 비육돈(F3)과 육성돈(F2)에서 금기(t)의 도축 마릿수(SLt)를 제외하도록 모형화 하였다. 이 변수들을 하나로 통합한 설명변수 $F3_{t-1}, + 0.45 F2_{t} − 1− SL_{t}$의 계수는 1로 추정되었다. 탄성치의 의미는 전월 비육돈(F3)이 1마리 증가하면 1마리, 전월 육성돈(4개월령)에서 당월 비육돈(5개월령)으로 넘어오는 전월 육성돈(F2)이 1마리 증가하면 0.45마리 증가하고, 당월 도축 마릿수가 1마리 증가하면 1마리 감소한다는 의미이다. 지금까지 추정한 단일방정식의 주요 탄성치의 요약은 아래 Table 11와 같다.
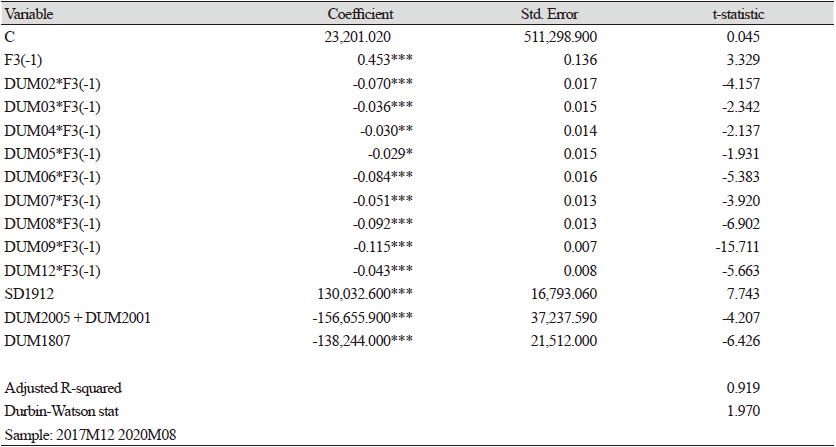
Table 12에서, 도축마릿수(SL)는 전월의 5 - 6개월령 비육돈(F3)의 함수로 구성하고, 여기에 기울기(slope) 계절 더미를 곱하였다. 이는 절편(shift) 더미보다 기울기(slope) 더미가 통계적으로 유의하였기 때문이다. 즉 Table 13과 같이, 계절별로 기울기가 다르게 추정되었다. 계절더미가 없는 1, 10, 11월은 계수는 0.45로 추정되어, 1개월 전 비육돈(F3)이 한 마리 증가할 경우, 당월의 도축마릿수는 0.45 마리 증가하는 것으로 추정되었다. 이와 같은 해석은 비육돈(F3)의 육성 단계별 기간이 2개월로 구분되기 때문이며, 생육행태와 일치하는 것으로 판단된다. 즉, 비육돈(F3)이 2개월동안 대부분 도축(0.45*2 = 0.9)되는 것으로 해석된다. 계절별로는 3, 4, 5, 7, 12월의 계수는 0.4 이상으로 추정되었는데, 3월, 4, 5월의 계수는 0.42수준으로, 7월은 0.40, 12월은 0.41로 추정되었다.
예측력 검정
예측력 검정 방법 중 하나인 Theil의 불평등 계수(coefficient of inequality)는 통계적 예측 평가치(statistical forecasting evaluators)로 자주 사용되나, Theil 자신이 동일한 이름 하에서 서로 다른 시간을 사용한 두 가지 수식을 제안함으로써, 약간의 혼란이 있는 계수이다. 같은 이름으로 서로 다른 학회에서 발표한 두 가지 수식 모두 불평등 계수(coefficient of inequality)라고 사용하고, “U”라는 기호로 표시된다. 우선적으로 “Economic Policy and Forecast”학회지에서는 U1을 제안하였고, “Applied Economic Forecasting” 학회지에서는 U2를 제안하였다(Ahlburg, 1984). 불평등 계수(coefficient of inequality) U1과 U2의 차이점은 분모에 있는 Ft의 존재 여부에 있고, Ft의 유무는 U1을 0과 1 사이로 제한하게 된다. 그러나 U2에서 Ft 항이 부재하여 U2에서는 유한한 상한선이 없다. 여기서는 U 가 0에 가까울수록 예측력이 좋다는 의미이다(Ahlburg, 1984).
$ U_{1} = \frac{\lbrack\frac{1}{n} \sum_{t = 1}^{n} (A_{t} - F_{t})^2\rbrack^{1/2}}{\lbrack \frac{1}{n} \sum_{t = 1}^{n} A_{t}^2\rbrack^{1/2} + \lbrack \frac{1}{n} \sum_{t = 1}^{n} F_{t}^2\rbrack^{1/2}} , U_{2} = \frac{\lbrack\sum_{t = 1}^{n}(F_{t} - A_{t})^2\rbrack^{1/2}} {\lbrack\sum_{t = 1}^{n} A_{t}^2\rbrack^{1/2}} $ (14)
본 연구에서 Hong 등(2020)과 Han 등(2021)과 같은 방법으로, Theil 불평등계수 추정은 전체 추정 기간 와 최근 1년을 구분하여 추정을 하였다. 이렇게 구분함으로써 추정된 모형의 예측력을 더욱 잘 설명할 수 있는 장점이 있다. Table 14과 같이 추정한 결과, Theil U1이 모든 함수에 있어서 0.011로 매우 낮게 추정되어, 예측력이 우수한 것으로 판단된다. 특히, 최근 1년간(12개월)의 Theil U1는 평균 0.004으로 예측력이 높게 나타났다. 이는 생물학적 성장 및 출하 시간을 고려한 코호트 및 동태적 생태방정식모형 체계(dynamic ecological equation model system)로 구축한 모형 설계와 이력제 데이터가 우수했던 것으로 판단된다.
Conclusion
본 연구의 목적은 축산물품질평가원의 월별 시계열자료인 한돈 이력제 데이터의 활용성에 대한 평가와 시사점을 도출하고, 이력제 데이터를 이용하여, 돼지의 임신, 출생과 성장, 도축 등 시차를 고려한 생육단계별 생물학적 특성을 반영한 코호트(cohort) 기법과 동태적 생태방정식 모형(DEEM) 체계를 구축하여 미래 출하 가능 마릿수 및 공급량을 예측하고, 경제이론에 부합된 정책 시뮬레이션이 가능한 월별 한돈모형을 구축하는데 있다. 다만, 이력제 데이터에 국한되어 공급측면의 모형구축에만 집중하였다.
이력제 데이터의 활용성에대한 검증결과, 모돈(PS)마릿수는 전체 약 6%에 해당되는 농장은 GGP, GP, PS, AI를 혼용하여 생산되기 때문에 사업형태별로 분리해야하는 보완작업이 필요한 한계점이 존재하였다. 따라서 본 연구에서 제안한 사업형태별로 모돈 마릿수 추정방법을 활용하여 GGP, GP, PS 데이터를 구축할 필요성이 있다. 또한, 비육돈 데이터에서는 폐사율 데이터가 존재하지 않았고, 비육돈(5 - 6개월)/육성돈(3 - 4개월) 비율은 폐사율을 감안한다고 하더라도 1.0보다 높게 나타나, 5 - 6개월 비육돈 이력제 데이터에는 6개월 이상의 비육돈 마릿수도 포함된 것으로 추정되어, 6개월령 이상 분리하거나, 데이터에 데이터 성격을 명확히 명시하는 등 보완작업이 필요하다.
이력제 데이터를 이용하여 모형추정결과, 종돈(GP)에서 후보돈, 모돈(PS)그리고 자돈 및 비육돈, 출하 등 돼지의 임신, 출생과 성장, 도축 등 시차를 고려한 생육단계별 생물학적 특성을 고려하여 추정된 계수 값이 돼지 생육행태와 모두 일치하는 것으로 분석되었다. 또한 모형 예측력 검정도 우수하게 나타났다. 이는 생물학적 성장 및 출하 시간을 고려한 코호트 및 동태적 생태방정식모형 체계(dynamic ecological equation model system)로 구축한 모형 설계와 이력제 데이터가 활용 측면에 있어 우수했던 것으로 판단된다.
마지막으로 본 연구에서 구축된 모형을 기반으로 생산자의 의사결정과 정부의 수급 관련 정책 방향을 설정하는 기초자료로 활용되기를 기대하며, 수요측면의 연구는 추후 연구과제로 남겨둔다.