Introduction
한우는 종자의 국외 의존도가 높은 타 품종과 달리 우리나라 고유의 품종을 가지는 대표적인 품종이다. 한우는 육용가축으로 경제형질 위주의 개량이 활발히 이루어져 있으며, 우선시 되는 특징은 번식 효율과 생시 체중, 이유 시 체중 등이다. 생시 체중과 이유 시 체중은 성장 능력에 관계되므로 중요한 요소라 할 수 있다. 그러나 세계 3대 육용종인 Hereford, Brahman 및 Aberdeen
angus 수소의 성숙 체중은 각각 950 kg, 900 kg 및 800 kg인 것에 반해 한우 수소의 성숙 체중은 650 kg으로 비교적 낮은 체중을 보인다. 그래서 한우는 다른 육우 품종에 비해 성숙 체중이 작고 성숙 체중에 도달하는 시기도 늦다는 점이 큰 단점으로 지적되고 있다(Lee et al. 2003b).
가축개량관련자료(Rural development administration, 2015)에서 체중 증가 및 고급육 생산으로 연간 2,109억 원의 효과를 거두고 있다고 보고된 바 있다. 그러나 현재 한우 거세우의 1등급 이상 출현율이 약 83% 이상으로(2016. 04. 축산물 등급 판정 통계) 고급육에 대한 개량은 충분히 이루어졌으며 체중에 대한 개량이 농가 수익 증대의 중요 요소로 대두되고 있다. 또한 가축개량관련자료(Rural development administration, 2015)에서 한우 18개월령 수소 체중은 매년 9.8 kg씩 증가하고 있고 유전적으로 한우 도체중은 매년 0.89 kg씩 증가하고 있는 추세 보인다고 보고한 바 있다. 그리고 이러한 육량 증가 효과로 연간 557억 원의 수익 증가를 보인다고 보고한 바 있다. 따라서 체중의 증가로 농가의 수익 증대뿐만 아니라 축산업 전반의 성장을 기대할 수 있다.
성장곡선은 경험적 모델의 시간에 따른 양의 진화로 생물학과 인구통계학 그 이외에 다양한 분야에서 널리 쓰이고 있는 추정 방법이다. 육종 통계 분야에서는 가축의 연령에 따른 체중의 변화를 추정하는 데에 사용되고 있다. 우수한 개체들의 체중에 대한 성장곡선을 추정하는 것은 농가에서 편리하게 체중을 추정할 수 있도록 하여 관리 경영상 뚜렷한 개선을 제공한다(Cho et al., 2006). 그리고 세대를 거듭한 개체들의 개량으로 인해 경제 형질 능력이 변화하기 때문에 이러한 변화에 따른 개정된 성장곡선이 계속해서 요구된다. 따라서, 체중 개량에 대한 중요성이 대두되고 있으며 개량의 효과로 인한 체중의 꾸준한 증가 현상으로 인해 체중에 대한 개정된 한우 거세우의 성장곡선 모형의 추정에 대한 필요성이 요구되고 있다.
국내에서 한우 수소나 거세우의 체중 자료로 비선형의 성장곡선 모형을 이용하여 성장곡선을 추정하는 연구가 Kim et al. (1996), Kim et al. (2002) 그리고 Cho et al. (2006) 에 의해 이루어 진 바 있다. Kim et al. (2002)은 28일 간격으로 6 - 30개월간 자료를 이용하여 거세우 성장곡선을 일령별로 거세우, 비거세우의 성장곡선을 비교하여 거세우의 성장 패턴이 암소와 유사하고, 24개월령에서 20%의 체중이 손실된다는 바를 보고하였다. 하지만 이 연구는 성장곡선의 효과분석 및 모수의 특성 등을 분석하였다.
Lee et al. (2003b)는 한우 암소는 생시 체중에 대한 성숙 체중 비율이 낮고 만숙성이며 변곡점 도달 시기가 빠르고 일당증체량이 작다고 보고하였다. Kim et al. (1996)의 연구에서는 Gompertz 모형과 Richard 모형 두 가지를 이용하였고, Lee et al. (2003a)의 연구에서는 암소의 성장곡선을 추정하는 등 여러가지 성장곡선 모형을 이용하여 한우에 적합한 성장곡선의 추정이 이루어진 바 있으나, 최근 주요 출하 품목인 한우 거세우에 대한 다양한 성장곡선을 추정하는 연구는 부족한 실정이다.
또한, 한우 거세우에 대해 Gompertz, Logistic 및 von Bertalanffy 3가지 성장곡선 모형을 통한 성장곡선 추정으로 가장 적합한 성장곡선을 추정하는 연구가 선행 연구에서는 진행된 바가 없어 본 연구는 개량된 체중을 고려한 최근 자료로 성장곡선을 추정하여 현재 한우 거세우에 가장 적합한 성장곡선을 추정함으로써 농가에서 연령에 따른 체중 파악 및 적정 출하시기 결정을 통한 비육우 관리에 활용하며 한우 농가 수입증대를 위한 한우 개량 방향 제시를 위한 기초자료로 활용하기 위해 연구를 진행하였다.
Materials and Methods
공시재료
성장곡선 추정을 위한 자료는 한우개량사업소 후대검정우의 출생일령을 기준으로 1989년부터 2015년까지 수집된 후대검정 자료로 총 6,973두의 성장을 기록한 것이다. 이 자료는 생시 체중을 측정한 6개월령, 9개월령, 12개월령, 15개월령, 18개월령, 21개월령, 24개월령의 체중 자료로 개체마다 측정 일령의 차이가 있다. 자료 중 측정치가 없는 자료는 모두 제거하였고, 개체의 성숙에도 불구하고 체중이 감소하는 측정치는 이상치로 간주하여 제거하여 사용하였고 모수를 추정하였다. 또한, 측정일을 기준으로 각각의 개체를 월령별로 분류하여 평균 체중에서 표준편차 ± 3배 이상을 벗어나는 자료는 이상치로 간주하여 제외하였다.
비선형 모델
체중에 대한 성장곡선 함수는 SAS 9.4의 PROC NLIN을 이용하여 Gauss-Newton법으로 추정하였다. 체중 성장곡선 추정에 이용되는 모형은 Gompertz 모형(Winsor, 1932), Logistic 모형(Nelder, 1961), von Bertalanffy 모형(von Bertalanffy, 1957), Richard 모형(Richards, 1959), Brody 모형(Brody, 1945) 등이 있다. 하지만, 본 연구의 성장곡선 모수 추정에는 Gompertz, Logistic, von Bertalanffy의 3가지 모형을 이용하여 모수를 추정하였다. 3가지 모형은 모두 선형의 s자 형태의 sigmoid 성장 형태를 보이며, 기본적인 sigmoid 곡선은 0과 1에 무한히 가까워지는 형태로 미분이 가능하며 변곡점이 존재한다.
von Bertalanffy 모형과 Logistic 모형의 경우 Brown et al. (1976)의 연구에서 Fashola Stock farm 의 26,818두 체중과 연령 자료를 이용한 성장곡선 추정 결과 초기 체중은 하향 추정되고, 성숙 체중은 상향 추정되는 경향이 있다고 보고 된 바 있다(Brown, 1976). Richard 모형은 추가로 변곡점 조절 모수 설정이 필요하므로 모수 추정이 번거롭고, 모수간의 높은 상관관계로 인해 실제 계산 시 추정치의 수렴이 곤란한 단점을 가진다(Cho et al., 2004).
(1) Gompertz 모형
Gompertz 모형의 변곡점은 성숙치의 1/3에 위치한다. 함수식은 다음과 같다.
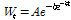
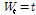 시점의 체중
시점의 체중
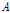 = 성숙체중에 관한 모수
= 성숙체중에 관한 모수
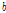 = 성장비율의 관한 모수
= 성장비율의 관한 모수
 = 성숙률에 관한 모수
= 성숙률에 관한 모수
 = 자연대수값
= 자연대수값
성장 곡선의 기울기가 최대가 되는 일령(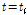 )인 변곡점(
)인 변곡점(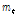 )은 성장곡선의 기울기 증가량이 양에서 음으로바뀌는 시기이며,
)은 성장곡선의 기울기 증가량이 양에서 음으로바뀌는 시기이며, 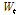 를 두번 미분한 다음 식으로 구할 수 있다.
를 두번 미분한 다음 식으로 구할 수 있다.
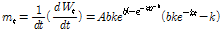
위의 식에서 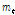 가 0이 되는
가 0이 되는 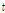 시기가 성장곡선의 변곡점이 된다.
시기가 성장곡선의 변곡점이 된다.
(2) Logistic 모형
Logistic 모형은 변곡점 조절 모수를 가지며, 변곡점 조절 모수에 의해 변곡점이 결정된다. 함수식은 다음과 같다.
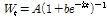
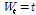 시점의 체중
시점의 체중
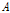 = 성숙체중에 관한 모수
= 성숙체중에 관한 모수
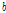 = 성장비율의 관한 모수
= 성장비율의 관한 모수
 = 성숙률에 관한 모수
= 성숙률에 관한 모수
 = 자연대수값
= 자연대수값
변곡점 조절 모수는 일반적으로 –1로 고정되어있다(Kim et al., 1996).
성장 곡선의 기울기가 최대가 되는 일령(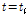 )인 변곡점(
)인 변곡점(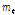 )은 다음 식으로 구할 수 있다.
)은 다음 식으로 구할 수 있다.
다음 식은 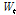 를 두번 미분하여 도출할 수 있다.
를 두번 미분하여 도출할 수 있다.
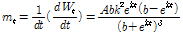
위의 식에서 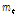 가 0이 되는
가 0이 되는 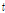 시기가 성장곡선의 변곡점이 된다.
시기가 성장곡선의 변곡점이 된다.
(3) von Bertalanffy 모형
von Bertalanffy 모형은 변곡점 조절 모수를 가지며, 변곡점 조절 모수에 의해 변곡점이 결정된다. 함수식은 다음과 같다.
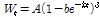
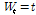 시점의 체중
시점의 체중
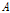 = 성숙체중에 관한 모수
= 성숙체중에 관한 모수
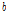 = 성장비율의 관한 모수
= 성장비율의 관한 모수
 = 성숙률에 관한 모수
= 성숙률에 관한 모수
 = 자연대수값
= 자연대수값
변곡점 조절 모수는 일반적으로 3으로 고정되어있다(Kim et al., 1996).
성장 곡선의 기울기가 최대가 되는 일령(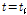 )인 변곡점은 다음 식으로 구할 수 있다.
)인 변곡점은 다음 식으로 구할 수 있다.
다음 식은 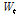 를 두번 미분하여 도출할 수 있다.
를 두번 미분하여 도출할 수 있다.
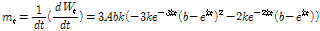
위의 식에서 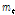 가 0이 되는
가 0이 되는 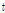 시기가 성장곡선의 변곡점이 된다.
시기가 성장곡선의 변곡점이 된다.
따라서 본 연구에서는 3가지 모형의 모수를 추정하여 성장곡선을 추정하고, 이를 실제 성장 체중과 비교하여 가장 적합도가 높은 성장곡선 모델을 추정한다.
Results and Discussion
자료 분포 특성
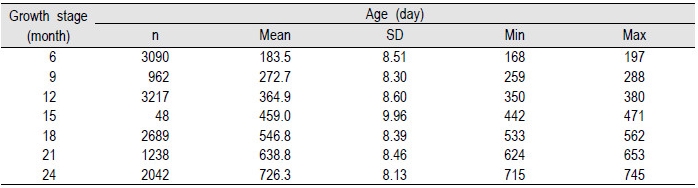
자료 중 측정치가 없는 자료를 제거하였고, 측정일을 기준으로 각각의 개체를 월령별로 분류하여 평균 체중에서 표준편차 ± 3배 이상의 이상치를 가지는 자료를 모두 제거하여 29,163개의 자료 분류하였다. 그리고 개체 별 체중이 감소하는 자료를 제거하여 총 29,086개의 데이터를 가지고 성장곡선을 분석하였다. Table 1 에 각 월령별 자료의 수와, 평균일령, 표준편차, 최대일령, 최소일령을 나타내었다.
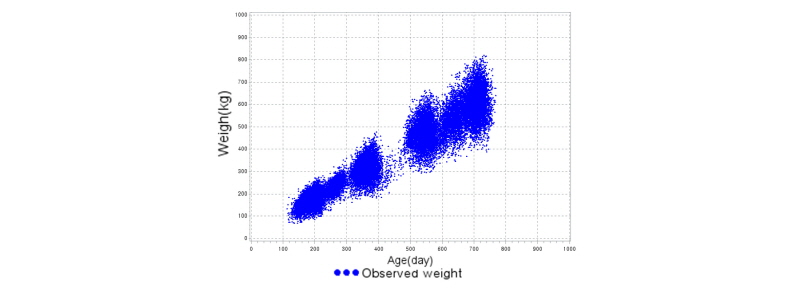
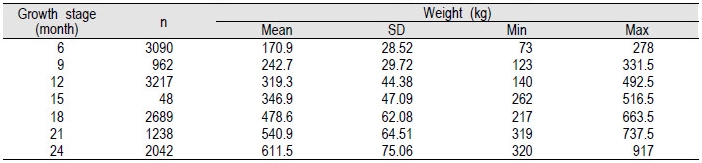
Fig. 1에서 전체 측정치의 일령에 따른 체중 분포도를 나타냈고 평균 체중의 그래프를 나타냈다. 자료의 분포는 sigmoid 형태를 나타내고 있다. 월령별 체중의 평균과 표준편차를 Table 2에 나타내었는데 체중의 평균은 성장함에 따라 꾸준히 증가하는 추세를 보이고 표준편차도 꾸준히 증가한다. 표준편차가 꾸준히 증가하는 것은 사육기간이 지남에 따라 사육 환경에 영향을 받아 체중의 편차가 커진 것으로 사료된다.
모델 별 모수 추정
일령별 체중에 대한 Gompertz 모형, Logistic 모형 및 von Bertalanffy 모형으로 추정한 성장곡선 모수와 각 모형의 평균 제곱 오차(MSE; mean square error)를 Table 3에 표시하였다.
본 연구는 성장곡선 모수 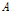 ,
, 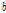 및
및  를 추정한 결과 Gompertz 모형은 각각 990.5 ± 10.27, 2.7479 ± 0.0068 및 0.00241 ± 0.000028로 추정됐다. 이는 Kim et al. (2002)이 한우 거세우와 비거세우의 성장곡선을 비교하여 거세우 각각의 모수를 추정한 823.1 ± 15.15, 3.301 ± 0.0489 및 0.0027 ± 0.00007과 비교해 볼 때 성숙체중에서 다소 차이를 보였다.
를 추정한 결과 Gompertz 모형은 각각 990.5 ± 10.27, 2.7479 ± 0.0068 및 0.00241 ± 0.000028로 추정됐다. 이는 Kim et al. (2002)이 한우 거세우와 비거세우의 성장곡선을 비교하여 거세우 각각의 모수를 추정한 823.1 ± 15.15, 3.301 ± 0.0489 및 0.0027 ± 0.00007과 비교해 볼 때 성숙체중에서 다소 차이를 보였다.
본 연구의 Logistic 모형의 모수 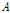 ,
, 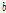 및
및  는 772.0 ± 4.12, 8.3314 ± 0.0453, 및 0.00475 ± 0.000033로 추정되었다. Cho et al. (2006)가 암소, 수소 와 거세우의 성장곡선을 비교한 연구에서 Logistic 모형으로 추정한 거세우의 모수는 각각 936.9 ± 51.27, 9.280 ± 0.294 및 0.003±0.0001으로 추정되었으며, 본 연구에 비하여 성숙 체중이 높은 결과를 보였다. Cho et al. (2006)는 모수 추정에서 거세우 60두의 일부 월령 자료가 없거나 부족한 상태로 분석되어 모수가 과대 추정된 것으로 보여진다.
는 772.0 ± 4.12, 8.3314 ± 0.0453, 및 0.00475 ± 0.000033로 추정되었다. Cho et al. (2006)가 암소, 수소 와 거세우의 성장곡선을 비교한 연구에서 Logistic 모형으로 추정한 거세우의 모수는 각각 936.9 ± 51.27, 9.280 ± 0.294 및 0.003±0.0001으로 추정되었으며, 본 연구에 비하여 성숙 체중이 높은 결과를 보였다. Cho et al. (2006)는 모수 추정에서 거세우 60두의 일부 월령 자료가 없거나 부족한 상태로 분석되어 모수가 과대 추정된 것으로 보여진다.
본 연구의 von Bertalanffy 모형의 모수 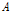 ,
, 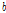 및
및  는 각각 1194.4 ± 18.39, 0.646 ± 0.005 및 0.00162 ± 0.000027로 추정되었다.
는 각각 1194.4 ± 18.39, 0.646 ± 0.005 및 0.00162 ± 0.000027로 추정되었다.
모델별 성장곡선의 추정
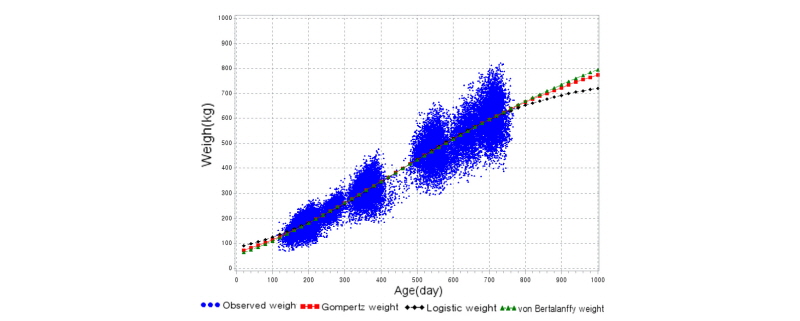
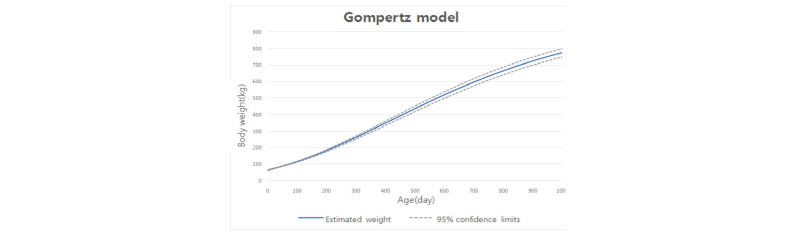
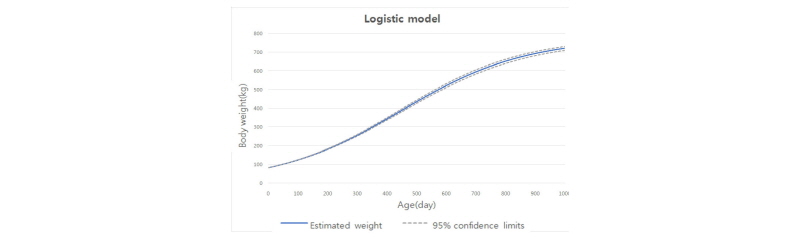
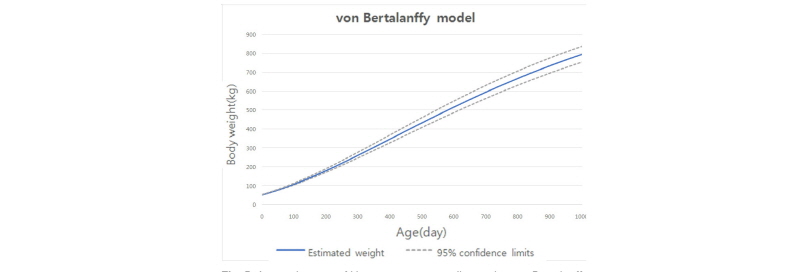
본 연구의 Gompertz 모형, Logistic 모형 및 von Bertalanffy 모형과 실제 자료의 분포도를 Fig. 2에 표시하였다. Gompertz 모형, Logistic 모형 및 von Bertalanffy 모형 모두 S자 형태의 sigmoid 성장곡선을 나타내었다. 3가지 그래프를 비교하였을 때 성숙 체중은 von Bertalanffy 모형이 가장 높았으며 Logistic 모형이 가장 낮았다. 초기체중은 von Bertalanffy모형이 가장 낮았으며 Logistic 모형이 가장 높게 추정되었다.
일령별 체중에 대한 Gompertz 모형, Logistic 모형 및 von Bertalanffy 모형의 변곡점을 각각 Fig. 3, Fig. 4 및 Fig. 5에 표시하였다. Kim et al. (2002)은 Gompertz 모형으로 성장곡선을 추정한 결과 거세우의 변곡점 일령은 444일이었으며, 변곡점에서의 체중은 302.8kg이라 보고하였다. Cho et al. (2006) 는 Gompertz 모형으로 성장곡선을 추정한 결과 거세우의 변곡점 체중은 385.9 kg이며, Logistic 모형의 변곡점 체중은 381.4 kg이라고 보고하였다. Fig. 3, Fig. 4 및 Fig. 5에서 변곡점은 각각 성숙체중에 대해 36.7%, 49.9% 및 29.9% 지점에 위치한다. Table 4에서 Gompertz 모형의 변곡점 일령은 421일이며, 변곡점에서 체중은 365.3 kg 이었다. Logistic 모형의 변곡점 일령은 445일이며, 변곡점에서의 체중은 385.0 kg 이었다. von Bertalanffy 모형의 변곡점 일령은 405일이며, 이때의 체중은 352.0 kg 로 추정되었다. 본 연구의 Gompertz 모형의 변곡점 일령과 체중은 Kim et al. (2002)이 보고한 자료보다는 일령은 낮게, 체중은 높게 나타난 바를 보아 Kim et al. (2002)이 추정한 시기보다 한우가 비육 중심으로 개량되어 초기 성장률이 증가한 결과로 보인다. 본 연구의 Logistic 변곡점 일령과 체중은 Cho et al. (2006)가 보고한 자료보다는 체중이 높게 추정되었다. 이 또한 본 연구가 개량된 최근 자료가 포함되었기 때문으로 사료된다.
Table 4. Inflection point age and weight of growth curves of Hanwoo steers according to the three models.
|
일반적인 사양관리 방법으로 12 - 13개월령을 경계로 육성기와 비육기로 구분된다. 본 연구에서 추정한 3가지 모델의 성장곡선의 변곡점 월령은 Gompertz 모형, Logistic 모형 및 von Bertalanffy 모형은 각각 14.0개월, 14.8개월 및 13.5 개월령으로 추정되었으며 이는 육성기와 비육기를 구분하는 시기와 유사하며, 변곡점 이전에는 체중 증가량이 증가하는 추세이기 때문에 변곡점 이전에 체중증가를 위한 사양 관리에 집중하고 변곡점 이후에는 체중의 증가량은 감소하는 추세를 보이기 때문에 체중증가보다는 육질 향상을 위한 사양 관리에 집중해야 한다고 사료된다.
모델별 실제 체중과의 비교
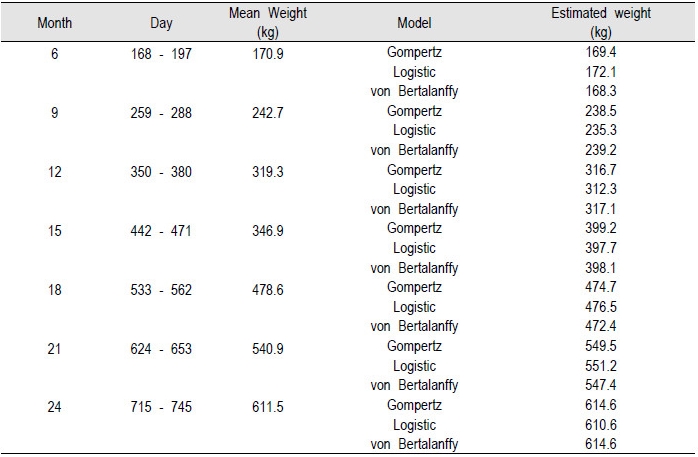
3가지 성장곡선 추정 모델 중에서 가장 적합한 모델을 추정하기 위하여 Table 5에 측정월령별 실제 평균 체중과 각 모델별 추정 체중을 표시하였다.
6개월령, 15개월령, 18개월령 및 24개월령의 실제 측정 체중의 평균과는 Logistic 모형 추정 체중이 가장 근접하였으며, 9개월령, 12개월령 및 21개월령의 실제 측정 체중의 평균과는 von Bertalanffy 모형이 근접하였다. 그러나 Logistic 모형과 von Bertalanffy 모형의 실제 체중과 추정 체중의 차이는 모두 근소하였다. Table 3의 각 모델별 MSE 값을 보면 Gompertz 모형이 2749.1, Logistic 모형이 2762.1 및 von Bertalanffy 모형이 2748.5로 von Bertalanffy 모형이 가장 낮은 MSE (MSE; mean square error)를 가졌다. MSE는 평균제곱오차로 낮을수록 추정에 적합하기 때문에 von Bertalanffy 모형이 성장곡선 추정에 가장 적합하다 사료된다.
Brown et al. (1976)은 von Bertalanffy 모형, Gompertz 모형, Brody 모형, Logistic 모형 및 Richard 모형으로 모형 간의 적합도를 비교 분석하였는데 그 결과 von Bertalanffy, Gompertz 모형 및 Logistic 모형에서는 성장 초기 체중이 높게 추정되고, Logistic 모형은 성숙체중이 다른 모형에 비해 작게 추정되는 경향이 보인다고 보고한 바 있다. 본 연구의 결과는 Fig. 2에서 보이듯이 Logistic 모형의 성숙체중이 von Bertalanffy 모형이나 Gompertz 모형보다 작게 추정되어 Brown et al. (1976)의 보고와 일치하는 성장곡선 추정이 이루어졌다고 판단된다.
모델별 출하 체중과의 비교
2015년 축산물 등급 판정 통계 연보에 따르면 한우 거세우의 평균 출하 체중은 720.6 kg 이고(농협음성축산물공판장 기준) 2014년 국립축산과학원 최신축산동향에 따르면 출하 두수의 분포는 31개월에 20.5%, 30개월에 18.7%로 가장 많다고 보고하였다. 따라서 평균 출하 체중과 출하 일령을 Table 6에 비교하였을 때 915일령 체중은 Gompertz 모형이 731.1 kg으로 가장 근접하였으며 von Bertalanffy 모형이 744.0 kg, Logistic 모형이 697.0 kg 순으로 근접하였다.
Table 6. Market weight and estimated market weight at 915 days of age according to the three models.
z Korea Institute for Animal Products Quality Evaluation. 2016.

|
각 월령별 실제 체중 평균과 추정 체중의 비교에서 Logistic 모형과 von Bertalanffy 모형이 많은 개월에서 근접한 추정치를 보였다. 출하 체중과 추정 출하 체중의 차이는 Gompertz 모형, von Bertalanffy 모형, Logistic 모형 순으로 적게 추정되었으며 von Bertalanffy 모형이 가장 낮은 MSE 값을 나타나기 때문에 본 연구를 통한 한우 성장곡선 추정에서는 von Bertalanffy 모형이 가장 적합한 모델이라 사료된다.
Conclusion
한우개량사업소 종모우의 출생 일령을 기준으로 1989년부터 2015년까지 수집된 후대검정 자료로 총 6,973두의 성장 기록을 이용하여 기존에 제안된 3가지 비선형의 성장곡선 모형을 사용하여 한우 거세우의 성장곡선 모형의 모수를 추정하고, 추정된 성장곡선모형의 모수를 이용하여 성장곡선을 추정하여 가장 적합한 성장곡선을 규명하기 위해 실시하였다.
각 성장곡선 함수로 추정한 한우 거세우의 성장곡선은 다음과 같다.
Gompertz 모형: 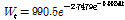
Logistic 모형: 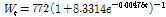
von Bertalanffy 모형: 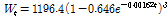
각 모형을 이용하여 추정된 성장곡선의 모수를 사용하여 성장곡선의 변곡점, 변곡점 일령, 변곡점에서의 체중 및 각 모형별 오차 제곱 합 등을 계산하였다. 세 모형 중 성숙 체중은 von Bertalanffy 모형이 1,196.4 kg으로 가장 크고, Gompertz 모형이 990.5 kg, Logistic 모형이 772.0 kg 순으로 추정되었다. 변곡점 도달 일령 또한 von Bertalanffy 모형이 405일로 가장 빨랐으며 Gompertz 모형이 421일, Logistic 모형이 445일 순으로 나타났다. 변곡점 도달 시 체중은 Logistic 모형이 385.0 kg으로 가장 크고, von Bertalanffy 모형은 352.0 kg으로 가장 작았다. 그리고 Gompertz 모형이 365.3 kg으로 추정되었다. 평균제곱오차는 von Bertalanffy 모형이 2,748.5로 가장 낮았고, Logistic 모형이 2,762.4로 가장 높았다. Gompertz 모형의 평균제곱오차는 2,748.1로 von Bertalanffy 모형과 근소한 차이를 보였다. 평균제곱오차는 낮을수록 추정에 적합하다. 각 월령별 실제 자료의 평균 체중과 추정 체중은 6개월령은 Logistic 모형, 9개월령과 12개월령은 von Bertalanffy 모형, 15개월령, 18개월령은 가 가장 근접하였다. 21개월령은 von Bertalanffy 모형, 24개월령은 Logistic 모형이 가장 근접하게 추정되었다.
실제 체중과 추정 체중의 차이는 Logistic 모형과 von Bertalanffy 모형이 가장 적었으나 두 모형 모두 실체 체중 평균과 차이의 크기가 크지 않고, 오차 평균 합이 Gompertz 모형이 가장 크고, von Bertalanffy 모형이 가장 낮은 결과로 볼 때, 본 연구의 자료인 한우 거세우의 성장은 von Bertalanffy 모형, Logistic 모형, Gompertz 모형 순으로 적합도가 좋은 것으로 판단된다.
Cho et al. (2006)의 보고에 따르면 체중기록뿐만 아니라 초기성장형태에 영향을 주는 환경적 요인에 대한 많은 정보가 필요하며 체중이 낮게 추정되는 6개월령까지의 초기자료뿐만 아니라 자료 크기, 사양 관리 등을 고려해야 보다 정확한 성장곡선 추정이 이루어진다고 하였다. 본 연구의 자료 역시 생시 체중 및 각 월령별 체중 측정치가 있지만 이들이 측정 월령과 일령에 다소 차이가 나고 약 15개령의 측정치가 다른 월령의 측정치보다 현저히 부족하여 성장곡선 추정에 어려움이 있었다. 좀 더 정확한 성장곡선 추정이 이루어지기 위해서는 여러 환경요인을 제거하여 성장곡선을 추정 할 수 있는 성장곡선추정모델의 개발이 필요한 것으로 사료된다. 또한 자료 역시 측정 및 기록 관리가 꾸준히 이루어져 누락된 자료가 없어야 하며 정확한 측정치가 필요할 것으로 판단된다.



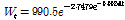 , the Logistic growth curve model equation was
, the Logistic growth curve model equation was 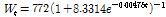 , and the von Bertalanffy growth curve model equation was
, and the von Bertalanffy growth curve model equation was 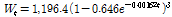 . The Gompertz model parameters A, b, and k were estimated to be 990.5 ± 10.27, 2.7479 ± 0.0068, and 0.00241 ± 0.000028, respectively. The inflection point age was estimated to be 421 days and the weight of inflection point was 365.3 kg. The Logistic model parameters A, b, and k were estimated to be 772.0 ± 4.12, 8.3314 ± 0.0453, and 0.00475 ± 0.000033, respectively. The inflection point age was estimated to be 445 days and the weight of inflection point was 385.0 kg. The von Bertalanffy model parameters A, b, and k were estimated to be 1196.4 ± 18.39, 0.646 ± 0.0010, and 0.00162 ± 0.000027, respectively. The inflection point age was estimated to be 405 days and the weight of inflection point was 352.0 kg. Mature body weight of the von Bertalanffy model was 1196.4 kg, the Gompertz model was 990.5 kg, and the Logistic model was 772.0 kg. The difference between actual and estimated weights was similar in the Logistic model and the von Bertalanffy model. The difference between market weight and estimated market weight was the lowest in the Gompertz model. The growth curve using the von Bertalanffy model showed the lowest mean square error.
. The Gompertz model parameters A, b, and k were estimated to be 990.5 ± 10.27, 2.7479 ± 0.0068, and 0.00241 ± 0.000028, respectively. The inflection point age was estimated to be 421 days and the weight of inflection point was 365.3 kg. The Logistic model parameters A, b, and k were estimated to be 772.0 ± 4.12, 8.3314 ± 0.0453, and 0.00475 ± 0.000033, respectively. The inflection point age was estimated to be 445 days and the weight of inflection point was 385.0 kg. The von Bertalanffy model parameters A, b, and k were estimated to be 1196.4 ± 18.39, 0.646 ± 0.0010, and 0.00162 ± 0.000027, respectively. The inflection point age was estimated to be 405 days and the weight of inflection point was 352.0 kg. Mature body weight of the von Bertalanffy model was 1196.4 kg, the Gompertz model was 990.5 kg, and the Logistic model was 772.0 kg. The difference between actual and estimated weights was similar in the Logistic model and the von Bertalanffy model. The difference between market weight and estimated market weight was the lowest in the Gompertz model. The growth curve using the von Bertalanffy model showed the lowest mean square error.